
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.8. Винтовые поверхности
Большую группу линейчатых неразвертывающихся поверхностей составляют винтовые поверхности (гелисоиды или геликоиды), имеющие широкое применение в технике.
Винтовые поверхности – это такие поверхности, у которых хотя бы одна направляющая – винтовая линия. В технике часто встречаются винтовые поверхности (рис. 7.23), образованные при винтовом движении прямой.
Такие поверхности образуются при движении произвольной образующей по винтовой направляющей. Если образующая – прямая линия, то образованные поверхности называются геликоидами.
В зависимости от величины угла наклона образующей к оси геликоиды бывают прямыми, если угол равен 90°, и наклонными (косыми), если угол – произвольный, отличный от 0 и 90°. Прямой геликоид образуется движением прямолинейной образующей i по двум направляющим: винтовой линии т и ее оси i; при этом образующая ℓ пересекает винтовую ось под прямым углом.
На рис. 7.23.а прямая линия iявляется осью винтовой линии или поверхности. Расстояние от точки 11 до оси i называется радиусом винтовой линии. Для построения винтовой линии в горизонтальной плоскости проекций один оборот разделился на 8 равных частей. В этих частях отмечены цифрами проекции положений точки. Высота подъёма разделена также на 8 частей. При повороте точки в горизонтальной плоскости проекций из положения 11 в положение 21 во фронтальной плоскости проекций точка из положения 12 переместится в положение 22 и так для каждого положения двигающейся точки. Соединяясь, все фиксированные положения точки образуют её фронтальную проекцию траектории движения.
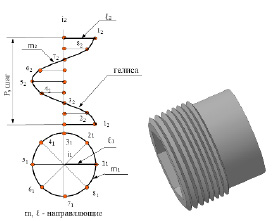
а б
Рис. 7.23. Пример построения (а) и использования (б) прямого геликоида
Горизонтальная проекция движения – окружность. Траектория движения называется винтовой линией. Винтовая линия постоянного радиуса называется гелисой. Величина подъёма винтовой линии за один оборот – её шаг. Если винтовую линию и ось i считать направляющими, а горизонтальную плоскость проекций за направляющую плоскость, то при движении прямолинейной образующей образуется винтовая поверхность, называемая прямым винтовым коноидом или геликоидом.
Геликоид, у которого образующая не перпендикулярна оси винтовой поверхности, называется наклонным или архимедовым.
Следует отметить одно важное свойство винтовых поверхностей, состоящее в том, что эти поверхности, так же как и поверхности вращения, могут сдвигаться, т. е., совершая винтовое перемещение, поверхность скользит вдоль самой себя. Это свойство обеспечивает винтовым поверхностям широкое применение в технике. Винты, шнеки, сверла, пружины, поверхности лопаток турбин и вентиляторов, рабочие органы судовых движителей, конструкции винтовых аппарелей и лестниц – вот далеко не полный перечень технического использования винтовых поверхностей. Кроме указанных в предложенном перечне, винтовые поверхности нашли широкое применение в строительстве и архитектуре.
Вопросы для самоконтроля
1. Как рассматриваются поверхности в начертательной геометрии?
2. Приведите краткую классификацию поверхностей, приняв за критерии классификации:
а) вид образующей;
б) характер перемещения образующей.
3. В чем сущность образования поверхностей кинематическим способом?
4. Что называется каркасом поверхности?
5. Чем отличается непрерывный каркас от дискретного?
6. Что является содержанием геометрической и алгоритмической частей определителя?
7. Как задается поверхность на эпюре Монжа?
8. Какие поверхности называются поверхностями Каталана?
9. Какие виды линейчатых поверхностей существуют?
10. Что такое очерк поверхности?
11. Как образуются поверхности вращения?
12. Укажите основные свойства поверхности вращения.
13. Как образуются винтовые поверхности?
14. По какому признаку поверхности геликоида подразделяют на закрытые и открытые?
15. Сформулировать признак принадлежности точки поверхности
16. Привести примеры использования различных поверхностей в технике, науке, искусстве и других видах деятельности человека.
[1] Тополόгия (от др.-греч. τόπος – место и λόγος – слово, учение) – раздел математики. Топология изучает: В самом общем виде – явление непрерывности; В частности – свойства пространств, которые остаются неизменными при непрерывных деформациях.
[2] Гомеоморфи́зм (греч. ομοιο – похожий, μορφη – форма) – взаимно однозначное и взаимно непрерывное отображение топологических пространств. Иными словами, это биекция, связывающая топологические структуры двух пространств, поскольку, при непрерывности биекции, образы и прообразы открытых подмножеств являются открытыми множествами, определяющими топологии соответствующих пространств.
[3] Гауссова кривизна – мера искривления поверхности в окрестности какой-либо её точки. Гауссова кривизна является объектом внутренней геометрии поверхностей, в частности, не изменяется при изометрических изгибаниях.
[4]Тензор – объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются векторы, билинейные формы и т.п.
