
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.1. Взаимное положение прямой и поверхности. Пересечение поверхности прямой линией
Одной из позиционных задач является определение взаимного положения прямой и поверхности.
Прямая может принадлежать поверхности и в этом случае все точки этой прямой принадлежат поверхности, а в другом случае прямая может пересекать поверхность и иметь точки входа и выхода (рис. 8.1).
а б
Рис. 8.1. Примеры пересечения прямой линией поверхностей:
а – втулки; б – диска
Для определения этих точек на комплексном чертеже можно использовать плоскости – посредники и использовать метод вспомогательных секущих плоскостей, сущность которого заключается в том, что через прямую ℓ проводится вспомогательная плоскость ∑ и на линииm пересечения этой плоскости с поверхностью λ находятся и точки входа и выхода А и В (рис. 8.2), принадлежащие прямой и поверхности.
Чтобы получить рациональное решение, следует использовать наиболее простой способ получения линии пересечения m. В качестве линии пересечения желательно получить либо прямую линию, либо окружность.
Рассмотрим некоторые примеры пересечения прямой линии с поверхностями.
m
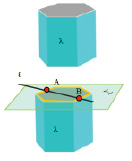
Рис. 8.2. Пример определения точек входа прямой ℓ в поверхность λ
и выхода из неё
Задача 1. Найти точки входа и выхода прямой ℓ при её пересечении поверхности пирамиды SАВС (рис. 8.3).
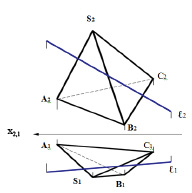
Рис. 8.3. Графическое условие задачи на определение
точек пересечения поверхности пирамиды прямой линией
Для решения предложенной задачи (рис. 8.3), нужно поступить так же, как при нахождении точки пересечения прямой с плоскостью (рис. 3.9): через фронтальную (горизонтальную) проекцию прямой ℓ2 провести вспомогательную проецирующую плоскость ∑, определить во фронтальной (горизонтальной) плоскости проекций точки пересечения вспомогательной плоскости с поверхностью пирамиды 12223242. Затем, по принадлежности, найти горизонтальную (фронтальную) проекцию линии пересечения 11213141 плоскости с поверхностью (рис. 8.4.а).
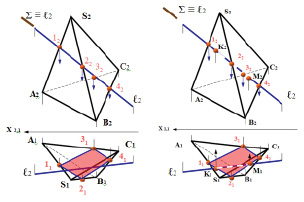
а б
Рис.8.4. Пример определения:
а – проекции линии пересечения поверхности плоскостью; б – точек входа
и выхода прямой при пересечении поверхности пирамиды
Для определения точек входа и выхода прямой при пересечении поверхности (рис. 8.4. б) необходимо в горизонтальной плоскости проекций найти горизонтальные проекции точек пересечения (К1 и М1) горизонтальной проекции прямой ℓ1 с горизонтальной проекцией линии пересечения поверхности с плоскостью 11213141. Затем по принадлежности определить фронтальные проекции (К2 и М2)точек входа и выхода. Часть линии, находящейся в поверхности будет невидимой.
Задача 2. Найти точки входа и выхода прямой АВ при её пересечении поверхности конуса (рис. 8.5).
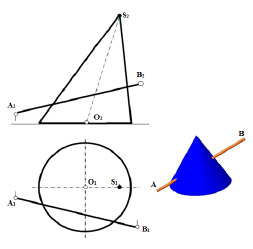
Рис. 8.5. Графическое условие задачи на определение точек входа и выхода
при пересечении поверхности конуса прямой линией
Для решения задачи нужно:
1) Во фронтальной плоскости проекций через прямую АВ и вершину конуса S провести вспомогательную произвольную плоскость, заданную двумя пересекающимися прямыми (SA, SB);
2) найти горизонтальный след h0 этой плоскости, для чего нужно построить два горизонтальных следа H и H’ прямых SA и SB вспомогательной плоскости (рис. 8.6).
3) Определить линию сечения поверхности вспомогательной плоскостью.
Горизонтальный след плоскости h0, пересекая основание поверхности конуса в точках 11 и 21, укажет границы проекции линии сечения (S11 21) поверхности вспомогательной плоскостью.
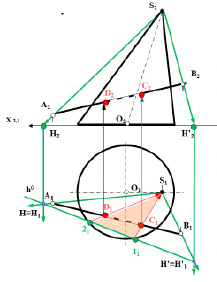
Рис. 8.6. Пример определения точек входа и выхода прямой
при пересечении поверхности конуса
4) Найти горизонтальные проекции точек входа и выхода.
Для определения точек входа и выхода прямой при пересечении поверхности конуса необходимо отметить горизонтальные проекции точек пересечения C1 и D1 горизонтальной проекции линии сечения поверхности конуса S11 21 с горизонтальной проекцией заданной прямой А1В1.
5) Определить фронтальные проекции точек входа и выхода.
Фронтальные проекции C2D2 точек входа и выхода прямой при пересечении поверхности конуса определяются по принадлежности. В соответствии с расположением прямой относительно поверхности определяется видимость элементов прямой.
Задача 3. Построить точки пересечения цилиндрической поверхности с прямой (рис. 8.7).
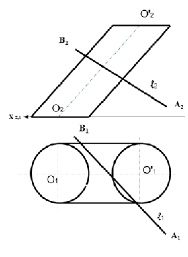

Рис. 8.7. Графическое условие задачи на пересечение поверхности цилиндра прямой линией
Для решения задачи нужно:
1) Во фронтальной плоскости проекций через прямую АВ провести произвольную вспомогательную плоскость, заданную двумя прямыми, параллельными образующим цилиндра;
2) Найти горизонтальный след h0 этой плоскости, для чего нужно построить два горизонтальных следа H и H’ параллельных прямых вспомогательной плоскости (рис. 8.8).
3) Определить проекции линии сечения.
Горизонтальный след плоскости h0, пересекая основание поверхности конуса в точках 11 и 21, укажет границы проекции линии сечения (111’1212’1) поверхности цилиндра вспомогательной плоскостью.
4) Найти горизонтальные проекции точек входа и выхода.
Для определения проекций точек входа и выхода прямой при пересечении поверхности цилиндра необходимо отметить горизонтальные проекции точек пересечения M1 и N1 горизонтальной проекции линии сечения поверхности цилиндра 111’1212’1 с горизонтальной проекцией заданной прямой А1В1.
5) Найти фронтальные проекции точек входа и выхода.
Фронтальные проекции N2M2 точек входа и выхода прямой при пересечении поверхности цилиндра определяются по принадлежности. В соответствии с расположением прямой относительно поверхности и плоскостей проекций необходимо определить видимость элементов прямой. В рассматриваемом случае фронтальная проекция точки N2 оказывается видимой, а проекция точки М2 – невидимой. Полное решение задачи представлено на рис. 8.8.
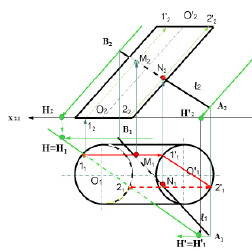
Рис. 8.8. Пример определения точек входа и выхода прямой
при пересечении поверхности цилиндра
Задача 4. Построить точки пересечения сферической поверхности с прямой (рис. 8.9).
Для решения такой задачи можно использовать способ замены плоскостей проекций. Через А1В1 провести вспомогательную горизонтально-проецирующую плоскость, которая позволит найти линию пересечения поверхность сферы.
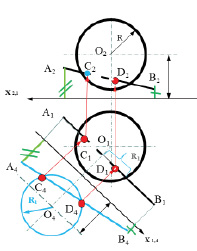
Рис. 8.9. Пример определения точек пересечения прямой
с поверхностью сферы на комплексном чертеже
Линия пересечения пройдёт по окружности радиуса R1. Натуральную величину линии сечения можно получить на плоскости проекций П4, параллельной вспомогательной плоскости сечения. Проекции точек входа и выхода прямой С4D4 в поверхности сферы окажутся на пересечении проекций линии сечения и прямой А4В4. По принадлежности находятся горизонтальные и фронтальные проекции точек С и D. Затем определяется видимость элементов прямой.
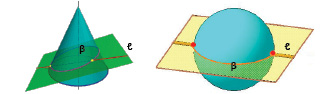
а б
Рис. 8.10. Примеры пересечения кривых поверхностей с прямыми линиями:
а – конуса; б – сферы
