
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.2. Пересечение поверхностей плоскостью
Определение взаимного положения плоскости и поверхности – задача позиционная, для решения которой применяется метод вспомогательных секущих плоскостей. В качестве вспомогательных секущих плоскостей используются проецирующие плоскости – плоскости перпендикулярные плоскостям проекций, поэтому основу метода вспомогательных секущих плоскостей составляет алгоритм решения задачи по нахождению проекций линии пересечения поверхности с проецирующей плоскостью.
Для определения проекций линии сечения следует найти проекции точек, принадлежащих этой линии.
В этом случае нужно выполнить анализ положений поверхности и плоскости относительно плоскостей проекций. Если секущая плоскость – общего положения, то необходимо её привести в проецирующее положение. Затем необходимо представить какого вида линия должна получиться в сечении и определить:
1) проекции опорных точек – точек расположенных на очерковых образующих поверхности (эти точки определяют границы видимости проекции кривой);
2) проекции экстремальных точек, удаленных на минимальные и максимальные расстояния от плоскостей проекций;
3) проекции произвольных (промежуточных) точек линии сечения.
В зависимости от положения плоскости по отношению к плоскостям проекций, сложность решения позиционной задачи, по определению линии пересечения ее с поверхностью существенно меняется. Наиболее простым представляется случай, когда плоскость проецирующая, а поверхность гранная. Решение подобной задачи рассмотрено на рис. 8.4.
Алгоритм решения таких задач однотипный. Рассмотрим задачи по определению линий сечения некоторых поверхностей.
Задача 1. Определить проекции линии сечения поверхности трёхгранной призмы с фронтально-проецирующей плоскостью λ (рис. 8.11).
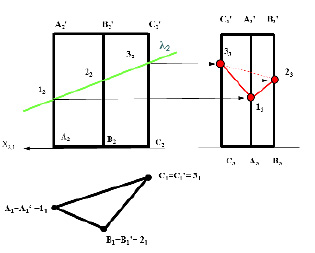

Рис. 8.11. Пример определения натуральной величины линии сечения
гранной поверхности проецирующей плоскостью
Многогранником называется пространственная фигура, ограниченная замкнутой поверхностью, состоящей из отсеков плоскостей, имеющих форму многоугольников. Стороны многоугольников образуют рёбра, а плоскости многоугольников – грани многогранника. Поэтому задачу по определению линии пересечения поверхности многогранника плоскостью можно свести к многократному решению задачи по нахождению: а) линии пересечения двух плоскостей (граней многогранника и секущей плоскости); б) точки встречи прямой (рёбер многогранника) с секущей плоскостью.
Если происходит пересечение многогранника, то в сечении должна получиться ломаная замкнутая кривая. В рассматриваемой задаче использован вариант а. Рассмотрим второй вариант.
Задача 2. Определить линию сечения пирамиды (рис. 8.12) плоскостью способом рёбер.
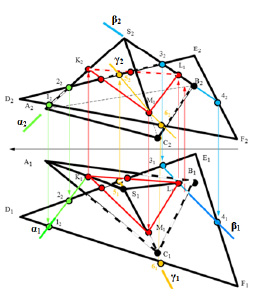
Рис. 8.12. Пример определения линии пересечения пирамиды с плоскостью
Для определения линии пересечения использованы вспомогательные проецирующие плоскости. Во фронтальной плоскости проекций через фронтальную проекцию ребра S2A2 проводится вспомогательная фронтально-проецирующая плоскость α, которая пересечёт фронтальные проекции сторон плоскости D2E2F2 в точках 12 22. По принадлежности определяются горизонтальные проекции 1121 этих точек и горизонтальная проекция точки K1 пересечения этой плоскости с ребром пирамиды S2A2. Фронтальная проекция К2 находится по принадлежности ребру S2A2. Аналогичными построениями находятся проекции точек L и M. Точка L находится с помощью плоскости β. Точка М находится с помощью вспомогательной горизонтально-проецирующей плоскости γ.
Особое место занимают задачи по нахождению линии пересечения плоскости с конической поверхностью. В зависимости от положения секущей плоскости линией пересечения может быть окружность, эллипс, парабола, гипербола (рис. 8.13).
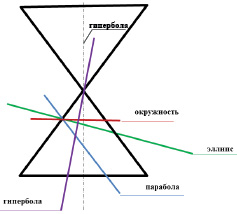
Рис. 8.13. Возможные линии сечения поверхности конуса плоскостью
Рассмотрим примеры пересечения поверхности конуса фронтально- проецирующими плоскостями.
Задача 3. Найти линию сечения поверхности конуса фронтально-проецирующей плоскостью (рис. 8.14).
Во фронтальной плоскости проекций фронтально-проецирующая плоскость λ, при пересечении обеих образующих поверхности конуса, даёт в сечении плоскую линию эллипса (рис. 8.14).
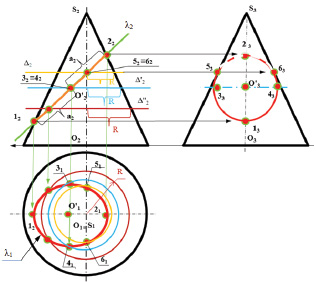
Рис. 8.14. Пример пересечения поверхности конуса
фронтально-проецирующей плоскостью
Для определения проекций этой линии сечения необходимо найти опорные точки, к которым относятся очерковые 12 и 22 (самая низкая и самая высокая), которые расположены на образующих конусной поверхности и представляют собой одну из проекций осей эллипса. В горизонтальной плоскости проекций проекции этих точек 11 и 21 расположены на осевой линии конуса. Вторая ось эллипса находится на середине оси 12 22 в точке О’2(12О’2 = О’222 = а). Эта ось определяет вторую пару опорных точек.
Одна из этих точек (41) является самой близкой. А вторая (31) – самой далёкой. Величина второй оси эллипса определяется с помощью вспомогательной плоскости уровня Δ’2, в сечении которой находится окружность радиуса R. Величина диаметра этой окружности 3141 и представляет величину второй оси этого эллипса. Последовательное соединение проекций, полученных точек, даёт возможность для определения проекций линии сечения поверхности плоскостью. Для определения добавочных (промежуточных) точек для построения линии сечения можно воспользоваться добавочными вспомогательными плоскостями. На рисунке 8.14. построения выделены цветными линиями.
При построении третьей проекции линии сечения нужно учесть, что проекции точек для построения определяются по принадлежности, а профильные проекции точек (53 63) являются точками смены видимости для проекции линии сечения в профильной плоскости проекций.
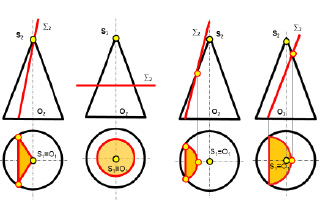
а б в г
Рис. 8.15. Примеры возможных линий сечений поверхности конуса:
а – треугольник; б – окружность; в – гипербола; г – парабола
Рассмотрим пример сечения конуса плоскостью, проходящей через вершину конуса и другие варианты сечений поверхности конуса.
При сечении конуса плоскостью, проходящей через вершину конуса, в сечении получится фигура треугольника (рис. 8.15 а).
В сечении конуса плоскостью, перпендикулярной оси конуса получится фигура окружности (рис. 8.15 б).
Если секущая плоскость наклонена к оси вращения конуса и не проходит через его вершину, то в сечении получатся линии: эллипса (рис. 8.15 б), параболы (рис.8.15 г) и гиперболы (рис. 8.15 в).
Если плоскость ∑ параллельна одной образующей поверхности конуса, то линией пересечения является парабола (рис.8.15 г). В частном случае (плоскость касательная к поверхности конуса) сечение вырождается впрямую.
Если плоскость ∑ параллельна двум образующим поверхности конуса (в частном случае параллельна оси конуса), то линия сечения будет гиперболой. В случае прохождения плоскости через вершину конической поверхности фигурой сечения могут быть сами образующие, т.е. гипербола вырождается в две пересекающие прямые.
Задача 4. Найти линию сечения поверхности сферы фронтально-проецирующей плоскостью (рис. 8.16).
Окружность, по которой плоскость α пересекает сферу, проецируется на плоскости П1 и П3 в виде эллипса, а на плоскость П2 в прямую линию, ограниченную очерком сферы.
Охарактеризуем выбранные для построения точки:
1, 2 – две вершины эллипса, определяющие положение малой оси на горизонтальной и профильной проекциях, их фронтальные проекции определяют пересечение следа плоскости ∑ с очерком сферы. Эти точки являются соответственно высшей и низшей точками сечения.
3, 4 – фронтальные проекции этих точек лежат на горизонтальной оси сферы, т.е. принадлежат экватору сферы, их горизонтальные проекции лежат на очерке сферы и определяют зону видимости при построении эллипса на П1.
5, 6 – фронтальные проекции этих точек лежат на вертикальной оси сферы, а профильные проекции лежат на очерке сферы и определяют зону видимости при построении эллипса на П3.
7, 8 – две вершины эллипса, определяющие положение его большой оси на горизонтальной и профильной проекциях.
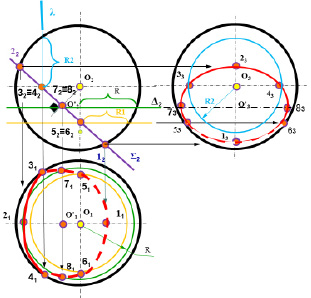
Рис. 8.16. Изображение пересечения поверхности сферы
проецирующей плоскостью
Положение их фронтальных проекций определяет перпендикуляр, опущенный из центра сферы к следу плоскости ∑.
Линия пересечения плоскости ∑ и сферы на фронтальной плоскости проекций совпадает со следом плоскости ∑, и на ней находятся точки 12 и 22. Горизонтальные проекции этих точек 11 и 21определяются с помощью линий связи на горизонтальной оси сферы в горизонтальной плоскости проекций.
Для определения промежуточных точек линии сечения, в общем случае, можно использовать вспомогательные секущие плоскости (Δ – горизонтальные плоскости уровня).
Например, через точки 52, 62, можно провести след плоскости Δ2 , на горизонтальной плоскости проекций линией пересечения вспомогательной плоскости сферы будет окружность радиуса R1. Горизонтальные проекции этих точек будут лежать на пересечении линии связи с полученной линией сечения. Для определения других промежуточных точек нужно выполнять аналогичные построения с использованием вспомогательных плоскостей (см. точки 71 и 81). Для определения точек 33и 43 удобно использовать вспомогательную плоскость λ. Эти проекции точек будут находиться на пересечении проекции линии сечения (окружность радиуса R2) cлиниями связи. Так могут находиться все проекции точек линии сечения.
Задача 5. Найти линию сечения поверхности цилиндра плоскостью, заданной следами (рис. 8.17).
Задача решается с помощью вспомогательных плоскостей ∑, проведённых через опорные точки поверхности цилиндра.
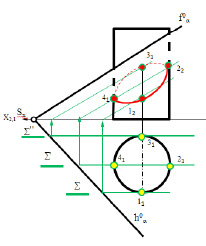
а б
Рис. 8.17. Пример определения линии сечения цилиндра плоскостью:
а – алгоритм определения; б – пример возможного результата определения
