
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
8.3. Взаимные пересечения поверхностей
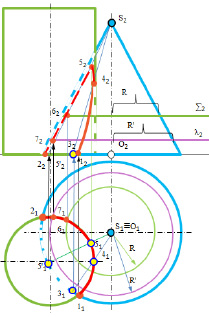
Построение линии пересечения поверхностей осуществляется при помощи вспомогательных секущих плоскостей, которые, пересекая поверхности, дают возможность определить точки линии пересечения поверхностей, которые, в рассматриваемом случае, принадлежат одной и той же вспомогательной плоскости и пересекающимся поверхностям (рис. 8.18).
а б
Рис. 8.18. Пример построения линии пересечения поверхностей конуса
и цилиндра с помощью вспомогательных секущих плоскостей:
а – алгоритм построения; б – пример возможного результата построения
При построении линии пересечения наиболее характерны два случая:
- одна из проекций линии пересечения известна и задача сводится к отысканию недостающих проекций точек по принадлежности одной из поверхностей;
- проекции линии пересечения не известны.
И в том и другом случае задача решается введением дополнительных секущих поверхностей, позволяющих находить точки, принадлежащие одновременно нескольким геометрическим объектам. В качестве дополнительных поверхностей могут использоваться плоскости, цилиндры и сферы, дающие наиболее простые (заранее известные) линии при пересечении с заданными поверхностями.
Если в качестве вспомогательных секущих поверхностей используются плоскости, то способ построения называют способом вспомогательных плоскостей.
Если используются сферы − способом вспомогательных сфер.
Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения цилиндра с конусом вращения (рис. 8.18).
Для построения линии пересечения заданных поверхностей удобно в качестве вспомогательных поверхностей использовать серию горизонтальных плоскостей, перпендикулярных оси конуса, которые пересекают цилиндр и конус по окружностям. На пересечении этих окружностей находят точки искомой линии пересечения.
Известно, что если ось поверхности вращения проходит через центр сферы и сфера пересекает эту поверхность, то линия пересечения сферы и поверхности вращения − окружность, плоскость которой перпендикулярна оси поверхности вращения. При этом, если ось поверхности вращения параллельна плоскости проекций, то линия пересечения на эту плоскость проецируется в отрезок прямой линии. Это свойство используют для построения линии взаимного пересечения двух поверхностей вращения с помощью вспомогательных сфер. При этом могут быть использованы концентрические и эксцентрические сферы. Рассмотрим применение вспомогательных концентрических сфер − сфер с постоянным центром (рис. 8.19).
Способ секущих сфер с постоянным центром для построения линии пересечения двух поверхностей применяют при следующих условиях:
- обе линии пересекающиеся поверхности − поверхности вращения;
- оси поверхностей вращения пересекаются;
- точку пересечения принимают за центр вспомогательных (концентрических) сфер;
- плоскость, образованная осями поверхностей (плоскость симметрии), должна быть параллельна плоскости проекций.
В случае, если это условие не соблюдается, то, чтобы его обеспечить, прибегают к способам преобразования чертежа.
а б
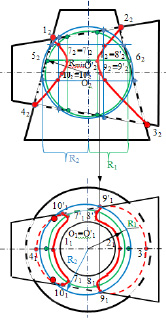
Рис. 8.19. Пример построения линии пересечения поверхностей конусов
с помощью концентрических сфер:
а) алгоритм построения; б) пример возможного результата построения
Такие сферы применяют, если:
- одна из пересекающихся поверхностей – поверхность вращения, другая поверхность имеет круговые сечения;
- две поверхности имеют общую плоскость симметрии (т. е. ось поверхности вращения и центры круговых сечений второй поверхности принадлежат одной плоскости – плоскости их симметрии).
Плоскость симметрии параллельна плоскости проекций (это условие при необходимости может быть обеспечено преобразованием чертежа). В этом случае окружности, по которым вспомогательные сферы пересекают поверхности, будут проецироваться на плоскость проекций в виде отрезков прямых. Для правильного использования метода вспомогательных секущих концентрических сфер рассмотрим задачу о пересечении двух конусов, оси которых пересекаются и параллельны П2.
В таком случае центром концентрических сфер, которые будут обеспечивать дополнительные построения, необходимые для решения задачи, принимается точка пересечения осей конусов.
Для решения задачи можно воспользоваться помощью вспомогательных сфер. Каждая из вспомогательных сфер может иметь по две пары отрезков параллельных основаниям конусов (за исключением применения минимального радиуса). Пересечение отрезков, принадлежащих разным конусам, даёт точки, принадлежащие линии пересечения поверхностей. Рассмотрим задачу, приведённую на рис. 8.19.
Фронтальные проекции 12, 22, 32, 42 точек находятся на пересечении фронтальных проекций очерков конусов. Их горизонтальные проекции 11, 21, 31, 41 находятся на горизонтальных проекциях осей конусов. Так как точки 3, 4 находятся на нижней очерковой линии, горизонтально расположенного конуса, их горизонтальные проекции – невидимые, а точки 1 и 2 – видимые. Для нахождения промежуточных точек линии пересечения поверхностей можно использовать концентрические сферы. Пересечение осей конусов даёт точку центра О2 концентрических сфер. Если из центра О2провести радиусом Rmin сферу, то в сечении конуса образуется окружность R1 (зеленого цвета).
На этой окружности образуются две пары промежуточных конкурирующих точек линии сечения 7 – 7’ и 8 – 8’, горизонтальные проекции которых находятся в проекционной связи с их фронтальными. Ещё две пары точек, искомой линии сечения, получаются аналогично рассмотренным (7 – 7’ и 8 – 8’) при использовании ещё одной концентрической сферы (синего цвета). В рассматриваемом примере линия пересечения конусов на фронтальной плоскости проекций П2 распалась на две видимые части относительно вертикальной осевой линии (127242, и 228232), а на горизонтальной плоскости проекций П1 эти части видны частично.
Точками смены видимости линии пересечения являются точки 9 и 10, которые находятся на образующих горизонтального конуса. На фронтальной плоскости проекции этих точек 92 – 9’2и 102 – 10 ‘2 расположены на оси. Горизонтальные проекции этих точек расположены на образующих горизонтально расположенного конуса и являются точками смены видимости на горизонтальной проекции линии пересечения двух рассматриваемых конусов.
Рассмотрим построение линии пересечения прямого кругового конуса и тора, оси которых скрещиваются с помощью эксцентрических сфер (рис. 8.20).
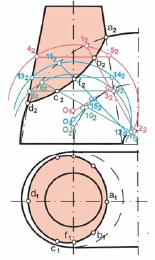
Ось конуса параллельна плоскости П2, ось тора перпендикулярна плоскости П2, окружность центров осевых круговых сечений тора и ось конуса лежат в одной плоскости, параллельной плоскости П2. Две очевидные характерные точки: высшая с проекцией а2 и низшая d2 – являются точками пересечения проекций очерков тора и конуса. Для построения проекций промежуточных точек, например проекции b2, выполняют следующие построения: выбирают на поверхности тора окружность, например с проекцией 12 22 с центром в точке с проекцией 32.
Перпендикуляр к плоскости этой окружности из точки с проекцией 32 является линией центров множества сфер, которые пересекают тор по окружности с проекцией 12 22. Из множества этих сфер выбирают сферу с центром на оси конуса. Его проекция О1. Эта сфера радиусом R1 пересекает конус по окружности с проекцией 42 52. Пересечение проекций 12 22 и 42 52 является проекцией пары общих точек тора и конуса, т.е. линии их пересечения. На чертеже обозначена проекция b2 одной из указанных точек – точки на видимом участке линии пересечения.
Построение проекций второй пары точек линии пересечения, из которых обозначена проекция c2, выполнено с помощью отрезка 62 72 − проекции окружности на поверхности тора. Вспомогательная сфера для построения проекции c2 − сфера радиусом R2 с центром, проекция которого О2. Конус эта сфера пересекает по окружности с проекцией 82 92. В пересечении проекций 62 72 и 82 92 окружностей находим проекцию c2 искомой точки и симметричной ей на невидимой части пересекающихся поверхностей.
а б
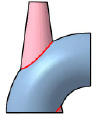
Рис. 8.20. Пример построения линии пересечения поверхностей конуса и тора
с помощью эксцентрических сфер:
а) алгоритм построения; б) пример возможного результата построения
Вопросы для самоконтроля
1) От каких параметров поверхности и плоскости зависит форма линии пересечения поверхности с плоскостью?
2) Каков алгоритм (порядок) определения линии пересечения поверхности плоскостью?
3) Какое положение плоскости пересечения по отношению к поверхности является предпочтительным для определения линии пересечения?
4) Какой способ построения линии пересечения называется способом вспомогательных сфер?
5) В каком случае при определении линии пересечения применяются концентрические (эксцентрические) сферы?
6) Какой способ построения линии пересечения необходимо применить, если две поверхности имеют общую плоскость симметрии?
7) Приведите пример определения линии пересечения поверхностей с помощью эксцентрических сфер.
