
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
9.1. Основные понятия и свойства
Поверхность называется развертывающейся, если она путем изгибания может быть совмещена с плоскостью без образования складок и разрывов. При этом нужно исходить из представления поверхности как гибкой, но нерастяжимой и несжимаемой пленки.
Построение разверток поверхностей представляет собой большое практическое значение при конструировании различных изделий для производства и, особенно часто, для изготовления конструкций, выполненных из листового материала способом изгибания. Из листового материала изготавливают, не только развертывающиеся поверхности, но и неразвертывающиеся поверхности. Неразвертывающуюся поверхность, в таком случае, можно разделить на части, которые можно заменить развертывающимися поверхностями, а затем выполнить отдельные развертки этих частей.
Свойством развертываемости обладают многогранные поверхности и кривые линейчатые поверхности с ребром возврата: торсы, конические и цилиндрические.
Линейчатые косые и нелинейчатые поверхности этим свойством не обладают. Существуют различные способы построения их условных разверток при помощи аппроксимации.
Если будем рассматривать поверхность и ее развертку как точечные множества, то между этими двумя множествами должно установиться взаимно однозначное соответствие и каждой точке на поверхности должна соответствовать единственная точка на развертке, каждой линии поверхности должна соответствовать линия на развертке и наоборот.
Плоская фигура, полученная в результате совмещения поверхности с плоскостью, называется разверткой (рис. 9.2).
Между поверхностью (рис. 9.1) и ее разверткой существует взаимно-однозначное точечное соответствие (точке А на поверхности соответствует точка А’ на развертке, и наоборот), обладающее следующими свойствами (рис. 9.2):
1) длина линии а на поверхности равна длине линии а’ соответствующей ей на развертке;
2) угол α° между кривыми m и n на поверхности равен углу α’° между соответствующими им кривыми m’ и n’ на развертке (углом между кривыми называется угол между касательными к ним в точке пересечения);
3) площадь отсека С поверхности равна площади соответствующего ему отсека С’ развертки.
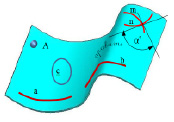
Рис. 9.1. Пример кривой поверхности
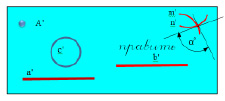
Рис. 9.2. Развёртка поверхности
В дифференциальной геометрии доказывается, что второе и третье свойства являются следствием первого. Первое свойство вытекает из представления поверхности как гибкой, но нерастяжимой и несжимаемой пленки.
Из рассмотренных свойств следует:
1) прямой линии (a) на поверхности соответствует прямая (а’) на развертке;
2) прямой линии b на поверхности соответствует прямая (b’) на развертке.
Однако оба указанных свойства обратной силы не имеют, т. е. не всякой прямой на развертке соответствует прямая на поверхности. Примерами этого могут служить цилиндрическая винтовая линия, параллели поверхности вращения.
Если кривой линии, принадлежащей поверхности, соответствует прямая на развертке, то эта кривая линия является геодезической для данной поверхности.
Геодезической называется линия, принадлежащая поверхности и соединяющая кратчайшим путем две точки, также принадлежащие поверхности.
