
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
9.5. Построение разверток кривых развертывающихся поверхностей
Необходимо отметить, что к развертывающимся поверхностям относятся только торсы (поверхности с ребром возврата, коническая и цилиндрическая поверхности).
Развертка любой развертывающейся поверхности (кроме гранных) является приближенной. Это можно объяснить тем, что при развертке такой поверхности ее аппроксимируют поверхностями вписанных или описанных многогранников, имеющих грани в форме прямоугольников или треугольников.
Поэтому при графическом выполнении развертки поверхности происходит спрямление кривых линий, принадлежащих поверхности, что и приводит к потере точности. Обычно строят приближенные развертки поверхностей, вполне пригодные для практических целей. Используя способ триангуляции необходимо определить истинные величины ребер вписанной пирамиды. Поверхность заменяется многогранной поверхностью, состоящей из треугольных граней. Рассмотрим применение способа триангуляции к построению развертки эллиптического конуса, изображенного на чертеже (рис. 9.5).
Триангуляция конической поверхности осуществляется вписыванием в нее пирамидальной поверхности, которая определяется ломаной 1 – 2 – 3 – 4, ..., вписанной в направляющую кривую конуса, и вершиной S. Развертка этой n-угольной пирамиды и принимается за развертку конуса. Все построения на чертеже (рис. 9.5) выполняются аналогично построениям на чертеже (рис. 9.3). Ломаная линия 1 – 2 – 3 – 4, ..., получающаяся на развертке пирамиды, заменяется плавной кривой, проходящей через те же точки.
При построении разверток цилиндрических поверхностей способ триангуляции, как правило, не применяется. Цилиндрическая поверхность заменяется (аппроксимируется) вписанной в нее призматической поверхностью.
.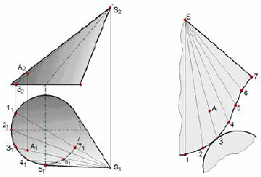
Рис. 9.5. Построение развертки эллиптического конуса
 .
.
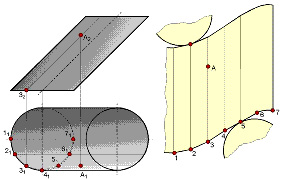
Рис. 9.6. Построение развертки цилиндрической поверхности
Эта поверхность определяется ломаной 1 – 2 – 3 – 4, ..., вписанной в направляющую кривую цилиндра, и направлением образующих. Развертка этой п-угольной призмы и принимается за развертку цилиндра (рис. 9.6). Все построения выполняются, как на рис. 9.2.
Ломаная линия 1 – 2 – 3 – 4, ..., получающаяся на развертке призмы, заменяется плавной кривой, проходящей через те же точки. Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник со сторонами, соответственно равными 2пr и h, где r – радиус окружности основания цилиндра, а h – его высота.
