Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

9.6. Построение условных разверток неразвертывающихся поверхностей

Развертку неразвертывающейся поверхности построить нельзя. Для построения условной развертки такой поверхности применяют метод аппроксимации, который заключается в следующем.

Данная неразвертывающаяся поверхность Ф разбивается на некоторые отсеки. Каждый из этих отсеков заменяется отсеком кривой развертывающейся поверхности. Совокупность всех отсеков развертывающихся поверхностей называется обводом Ф’ поверхности Ф. С помощью триангуляции обвод Ф’ заменяется обводом Ф» гранных поверхностей. Развертка гранных поверхностей, образующих обвод Ф», принимается за условную развертку поверхности Ф. При свертывании такой развертки, кроме изгибания, необходимо произвести частичное растяжение или сжатие отдельных ее участков.

Построение развертки сферы

Сферическая поверхность является неразвертывающейся. Существующие методы построения ее развертки дают лишь приближенные результаты. Сущность одного из них заключается в том, что элемент сферической поверхности заменяется элементом цилиндрической поверхности касательной к сфере по главному меридиану m. Ось такой цилиндрической поверхности проходит через центр сферы перпендикулярно G2. При этом под элементом сферы понимают часть ее, ограниченную двумя большими окружностями.

Для выполнения построения развертки поверхность сферы:

1) разделить большими окружностями на несколько (например, 6) равных частей. Каждый из образовавшихся элементов сферы проецируется на плоскость П1, в виде сектора;

2) описать вокруг сферы цилиндрическую поверхность, ось которой проходит через центр сферы перпендикулярно к П2;

3) заменить элемент сферы частью цилиндрической поверхности. Горизонтальной проекцией этого цилиндрического элемента окажется треугольник А1В1О1, а фронтальной – контур сферы (дуга окружности).

4) для построения развертки цилиндрического элемента (лепестка) разделить его фронтальную проекцию на восемь равных частей;

5) построить горизонтальные проекции образующих, соответствующих точкам деления. Истинные длины отрезков образующих для построения развертки взять с горизонтальной проекции (отрезки А1 В1, С1 D1, E1 F1, G1 H1) а расстояния между ними измерить на фронтальной проекции (расстояния между точками 1222, и 2232);

6) при построении цилиндрического элемента (лепестка) через середину отрезка АВ = А1В1 провести вертикальную ось симметрии лепестка, на которой отложить вверх и вниз четыре отрезка 10 –20 = 1222, 20 – 30 = 2232, 30 – 40 = 3242, 40 – 50 = 4252.

7) через точки 20, 30, 40 провести отрезки C0D0 = C1D1, E0F0, G0H0 = G1H1.

8) соединить плавной кривой концы отрезков, в результате чего получится развертка верхней половины лепестка.

При выполнении построения развертки часто возникает необходимость определить положение какой-либо точки на поверхности. Рассмотрим положение точки К на поверхности сферы и перенесем ее изображение на развертку. Это можно выполнить с помощью двух координат дуг S1 и S2. S2 показывает смещение точки К от экватора к полюсу, а дуга S1 − смещение ее от одного из меридианов по параллели сферы. Дуга S2 равна той части меридиана сферы, которая ограничена экватором и параллелью, проходящей через точку К (К2).

Длину этой дуги S2 = К2´М2 нужно откладывать на развертке от экватора соответствующего лепестка по вертикальной оси симметрии.

Строим развертку каждого сектора (лепестка) цилиндрической поверхности.

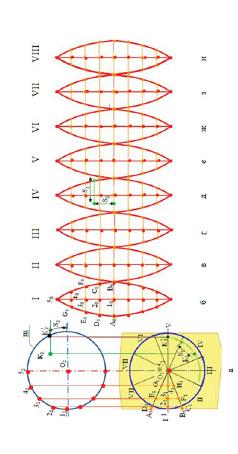
На чертеже (рис. 9.7, в) показана развертка одного из них. Затем ломаная 1 – 3 – 5 – 7... заменяется плавной кривой, проходящей через те же точки (рис. 9.7, г). Полученная фигура принимается за условную развертку сектора сферы.

Полная развертка сферы будет состоять из восьми таких фигур (рис. 9.7, д).

Doc36.pdf