
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
10.1. Основные положения
Касательные плоскости имеют большое значение в начертательной геометрии. С помощью касательных плоскостей можно определить направление нормали n к рассматриваемой поверхности β в точке касания М.
τ
а б
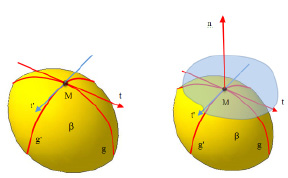
Рис. 10.1. Касательные к поверхности α:
а – прямая t , б – плоскость
Решение таких задач нашло широкое применение в инженерной практике и в архитектурном проектировании. С помощью касательных плоскостей выполняется построение очерка геометрических фигур, ограниченных замкнутыми поверхностями и при определении границы собственных теней.
Прямая линия t, касательная к какой-либо кривой линии g, принадлежащей поверхности, является касательной и к поверхности (рис. 10.1, а).
Плоскость τ, касательная к поверхности в заданной на поверхности точке М, есть множество всех прямых – касательных, проведенных к поверхности через данную точку. Через любую точку M поверхности β можно провести множество кривых, а, следовательно, и множество касательных прямых. Положение плоскости τ в пространстве определяется двумя пересекающимися прямыми, поэтому для построения касательной плоскости к поверхности в заданной точке достаточно построить касательные t и t’ к двум кривым линиям g и g’, проходящим через эту точку. В качестве таких кривых выбирают наиболее простые линии поверхности. Если данная поверхность является линейчатой, то за одну из таких кривых целесообразно взять прямолинейную образующую (касательная к прямой линии есть сама прямая).
Нормалью к поверхности в заданной точке называется прямая, которая перпендикулярна к касательной плоскости τ и проходящая через точку касания (рис. 10.1, б).
В дифференциальной геометрии доказано, что все эти касательные прямые располагаются в одной плоскости, которая называется касательной плоскостью (τ) к поверхности в данной ее точке (рис. 10.1, б).
Если через точку поверхности можно провести касательную плоскость и при том одну, то точка поверхности называется о б ы к н о в е н н о й, в другом случае – о с о б о й (например, вершина конической поверхности).
Касательная плоскость и кривая поверхность могут занимать различные положения относительно друг друга. При этом общим элементом может быть только элемент касания: либо точка М (рис. 10.1), либо линия, которая может быть прямой t (рис. 10.2) или кривой ℓ (рис. 10.3.б).
На рис. 10.1. касательная плоскость τ имеет с поверхностью β одну общую точку. При этом, все линии поверхности, пересекающиеся в этой точке, находятся с одной стороны от касательной плоскости и точка в этом случае называется эллиптической, а поверхности, у которых все точки эллиптические будут криволинейными и выпуклыми. К таким можно отнести поверхности сферы, тора, параболоида и эллипсоида.
Когда касательная плоскость имеет с поверхностью общую плоскую линию (прямую или кривую), точки, принадлежащие этой линии, называют параболическими (рис. 10.2, 10.3, б). Такие общие линии имеют поверхности цилиндра, конуса и тора и торса.
Для построения поверхности, соприкасающейся с рассматриваемой поверхностью вращения, используются соосные с заданной поверхностью цилиндр (рис. 10.3, а) и конус вращения.
а б
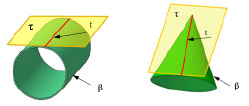
Рис. 10.2. Изображение касательных прямых на поверхности:
а – цилиндра, б – конуса
а б
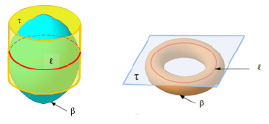
Рис. 10.3. Изображение касательных кривых линий на поверхности тора при касательной: а – поверхности цилиндра, б – плоскости
Когда касательная плоскость имеет с поверхностью общую точку и при этом пересекает поверхность по двум линиям, указанную точку называют г и п е р б о л и ч е с к о й, которая принадлежит линии, по которой касательная плоскость пересекает поверхность.
Каждый отсек поверхности, у которой все точки являются гиперболическими, имеют форму седлообразную. Если рассматривать касательную плоскость к поверхности однополосного гиперболоида (рис. 10.4), то можно отметить, что касательная плоскость τ, пересекает поверхность гиперболоида β в точке А по двум прямым a и b.
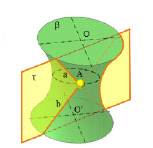
Рис. 10.4. Изображение касательной плоскости к гиперболической поверхности
Касательные плоскости к поверхностям можно провести, если при этом плоскость:
1 – касается поверхности в точке, ей принадлежащей;
2 – проходит через точку, лежащую вне поверхности;
3 – проходит через линию (прямую или кривую), принадлежащую поверхности;
4 – проходит через прямую, не принадлежащую поверхности;
5 – проходит параллельно прямой;
6 – проходит параллельно заданной плоскости.
