Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

10.2. Примеры построения касательной плоскости к поверхности

Построение плоскостей, касательных к поверхностям может быть выполнено различными способами и зависит от вида поверхности и условий задачи.

К таким способам можно отнести:

– построение касательных прямых к двум кривым линиям поверхности и проходящим через одну точку, принадлежащую поверхности (рис. 10.1);

– построение касательного следа плоскости к одноименному следу поверхности, который с линией касания определяет эту плоскость;

– построение вспомогательного сечения поверхности с проведением к нему касательной прямой определенного направления.

При решении рассмотренных выше задач на построение касательных плоскостей, используется положение о сохранении касания прямой к кривой линии в пространстве и в проекции.

Рассмотрим примеры построения касательных плоскостей к линейчатым поверхностям с параболическими точками. К таким поверхностям относятся поверхности конуса и цилиндра. В таких случаях касательная плоскость к поверхности в заданной её точке должна определяться двумя прямыми, касательными к двум пересекающимися в этой точке кривым линиям поверхности. Касательную плоскость к заданной точке для конуса и цилиндра можно определить двумя пересекающимися прямыми. Одна из этих прямых образующая, проходящая через заданную точку, а вторая является касательной к любой кривой линии поверхности, проходящей через заданную точку.

Пример 1. Построить касательную плоскость к поверхности конуса и проходящую через точку А, лежащую на его поверхности (рис. 10.5).

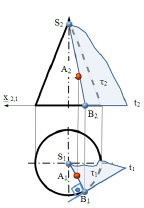
missing image file

Рис. 10.5. Построение касательной плоскости к поверхности конуса

В рассматриваемом случае касательную плоскость τ определяют образующая SB поверхности конуса проходящая через точку А, принадлежащую поверхности конуса и касательная t к очерку конуса в точке В на горизонтальной плоскости проекций П1. В примере касательная плоскость к поверхности конуса образована двумя пересекающимися прямыми τ (SB ∩ t).

Кроме рассмотренного выше примера существует и другой вариант.

Пример 2. Построить плоскость касательную к поверхности конуса и проходящую через точку С, не принадлежащую поверхности конуса (рис. 10.6).

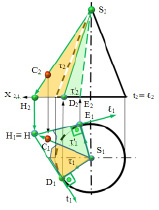
missing image file

Рис. 10.6. Касательные плоскости к конусу через точку,
не принадлежащую поверхности конуса

Для решения предложенного примера необходимо через вершину S и заданную точку С провести прямую SC и найти её горизонтальный след Н1. Через этот след необходимо провести две касательные линии t1 и ℓ1 к очерку касательной поверхности и получить две точки касания D, Е. Затем через эти точки провести образующие SD и SE (S1D1; S1E1и S2D2; S2E2). Пересечение рассмотренных образующих с касательными t1 и ℓ1 в точках D и E позволяет образовать две касательные плоскости к поверхности конуса τ(SD ∩ t) и τ’(SE ∩ ℓ1).

Пример 3. Построить плоскость, параллельную прямой d и касательную к конусу (рис. 10. 7).

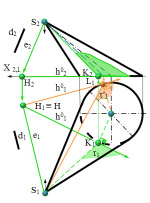
missing image file

Рис. 10.7. Плоскости касательные к конусу и параллельные прямой

Для выполнения предложенной задачи возможно построение двух плоскостей. Для этого через вершину конуса S параллельно заданной прямой d необходимо провести прямую e и построить её горизонтальный след на плоскости основания поверхности конуса. При этом необходимо отметить, что через этот горизонтальный след прямой e проходят два горизонтальных следа h01 плоскостей τ и τ’, касательных к поверхности конуса. Их точки касания К и L образуют касательные образующие SK и SL. На рис. 10.7 касательные плоскости обозначены разным цветом.

Пример 4. Построить плоскость, касательную к наклонному цилиндру и параллельную прямой d (рис. 10.8).

Для решения этой задачи нужно: через произвольную точку С провести две прямые, одна из которых е – параллельна образующим цилиндра, а вторая параллельна заданной прямой d; найти их горизонтальные следы Н(Н1, Н2) и Н’(Н’1, Н’2), которые определяют направление горизонтального следа h0 плоскости, параллельной касательной; параллельно этому следу провести следы двух касательных плоскостей τ и τ’ в точках касания K и L к цилиндру.

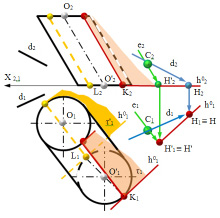
missing image file

Рис. 10.8. Пример построения касательных плоскостей к поверхности цилиндра

Пример 5. Построить плоскость касательную к поверхности вытянутого эллипсоида и проходящую через точку К, принадлежащую заданной поверхности (рис. 10.9).

Для решения задачи через точку К необходимо провести параллель поверхности и к ней касательную t. Фронтальная проекция этой касательной линии совпадёт с фронтальной проекцией параллели, а горизонтальная проекция этой касательной t1 будет касательной линией к окружности, т.е. горизонтальной проекцией параллели. За вторую кривую, проходящую через точку К можно принять имеющийся на чертеже главный меридиан (очерк фронтальной проекции эллипсоида), но для этого нужно представить, что заданный эллипсоид повернулся вокруг своей оси CD так, чтобы меридиан, проходящий через точку Е, занял положение главного меридиана СКD. При этом точка Е займет положение точки К. В этом случае, проведя касательную t’ к эллипсу, получим фронтальную проекцию второй касательной линии t’2 к эллипсоиду в точке Е. Следующим шагом построения должен быть поворот этой касательной таким образом, чтобы она прошла через точку К. Тогда точка S окажется на касательной линии t’ и на оси эллипсоида и останется без движения, направление горизонтальной проекции касательной линии t’1 к меридиану совпадёт с направлением S1K1.

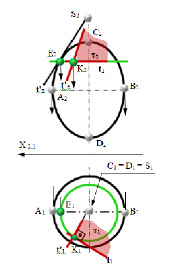
missing image file