Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.1. Моделирование и оптимизация одноканальных СМО
На рис. 2.1 представлен граф состояний для одноканальной системы, где для удобства состояния системы s0, s1, ..., sk, ... нумеруются по числу заявок, находящихся в СМО.
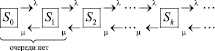
Рис. 2.1. Граф состояний для одноканальной СМО с неограниченной очередью
Система может находиться в одном из состояний:
s0 – канал свободен;
s1 – канал занят (обслуживает заявку), очереди нет;
s2 – канал занят, одна заявка стоит в очереди;
…
s – канал занят, (k – 1) заявок стоит в очереди;
…
По всем стрелкам поток заявок с интенсивностью λ переводит систему слева направо, а справа налево – поток обслуживания с интенсивность μ.
Основные характеристики рассматриваемых систем сведены в табл. 2 [3].
Таблица 2
Показатели работы СМО
|
№ п/п |
Наименование |
Характеристика/формула |
|
|
1 |
λ |
Интенсивность потока заявок |
Среднее число заявок, поступающих в СМО в единицу времени [число заявок/единицу времени] |
|
2 |
μ |
Интенсивность потока обслуживания |
Среднее число заявок, обслуживаемых в единицу времени [число заявок/единицу времени] |
|
3 |
ρ |
Приведенная интенсивность потока заявок (интенсивность нагрузки канала) |
Среднее число заявок, приходящее за среднее время обслуживания одной заявки
|
|
4 |
Ls |
Среднее число заявок в системе |
|
|
5 |
Lq |
Среднее число заявок в очереди (длина очереди) |
|
|
6 |
Среднее число заявок в канале (обслуживания) |
Ls – Lq = ρ |
|
|
7 |
Ts |
Среднее время пребывания заявки в системе |
|
|
8 |
Tq |
Среднее время ожидания в очереди |
|
|
9 |
Среднее время обслуживания |
|
|
|
10 |
γ |
Отношение времени ожидания в очереди к времени обслуживания |
|
Исследуем одноканальные системы массового обслуживания с очередью, на которую не наложено ограничений (ни по длине очереди, ни по времени ожидания) на примере входящего судопотока в морском порт, имеющий один канал – специализированный грузовой терминал и рейд для ожидания судов очереди на выполнение погрузочно-разгрузочных работ у терминала.
При проектировании новых портов с терминалом для обслуживания перспективного грузопотока (судопотока), а также для повышения эффективности функционирования существующих терминалов целесообразно предварительно построить имитационную модель системы, исследуя которую можно найти оптимальные параметры функционирования реальной системы. Таким образом, имитационная и оптимизационная составляющая модели должны составлять единый взаимоувязанный комплекс, обеспечивающий эффективное решение задачи минимизации приведенных совокупных затрат по эксплуатации терминала и по содержанию судов во время их пребывания в очереди и у терминала.
Моделирование систем массового обслуживания подчинено парадигме дискретно-событийного имитационного моделирования. Это совокупность операций или процессов с заявками, подчиненных причинно-следственным связям. На рис. 2.2 представлена процессная диаграмма одноканальной СМО [3].
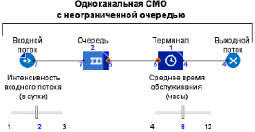
Рис. 2.2. Принципиальная схема одноканальной СМО
В одноканальной СМО с неограниченной очередью оптимизация подразумевает обеспечение такого соотношения интенсивностей поступления заявок (λ) и их обслуживания (m) при котором обеспечивается минимум суммарных (совокупных) затрат по ожиданию заявок в очереди и обслуживания в канале. Очевидно, эти совокупные затраты f определяются приведенной интенсивностью потока заявок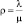 
(см. табл. 2), т.е. f = f(ρ). Ясно, что стремление минимизировать затраты, связанные с ожиданием в очереди, приводит к увеличению расходов в канале (обслуживания). И наоборот минимизация затрат на обслуживание заявок (увеличение интенсивности нагрузки канала) приведет к возрастанию времени (и соответственно затрат) ожидания в очереди.
В рассматриваемой проблеме параметром оптимизации является интенсивность нагрузки терминала, а целевой функцией – суммарные приведенные затраты по судам и терминалу [4].
Минимизация расходов по терминалу возможна при условии его полного использования (отсутствия свободных резервов), а это, в свою очередь, ведет к возрастанию простоев судов. С другой стороны, минимизация расходов по судам может быть обеспечена за счет увеличения пропускной способности терминала, однако это, очевидно, связано с дополнительными затратами по устройству и содержанию терминала
Затраты по судам могут быть найдены так:
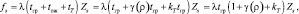(1)
|
где tгр, tож, tТ – |
соответственно длительность грузовых операций, их ожидания и технических операций; |
|
Zs – |
затраты по судну в сутки; |
|
kT – |
коэффициент, учитывающий время на выполнение технических операций на судне. |
Соответственно, затраты по терминалу:
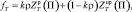(2)
|
где k – |
коэффициент, учитывающий перерывы между сменами, различные технологии работы и т.д.; |
|
П – |
пропускная способность терминала (т/сут). |
|
|
затраты по терминалу за время работы и простоя в сутки, соответственно. |
–
Сложив выражения (1) и (2) и разделив на планируемый грузооборот G = ρП получим суммарные приведенные затраты по судам и терминалу (УЕ/т):
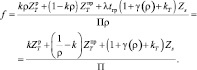
Таким образом в среде AnyLogic решается следующая экстремальная задача:
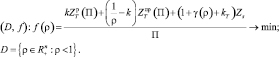
На рис. 2.3 представлены графики затрат по судну, терминалу их сумма и приведенных затрат в зависимости от интенсивности нагрузки терминала.
Увеличение пропускной способности терминала (П > G) приводит к увеличению затрат по терминалу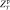 
и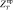 
и как следствие к уменьшению значения γ = γ(ρ), а следовательно и затрат по судам.
На рис. 2.4 представлена принципиальная расчетная схема определения основных показателей функционирования системы.
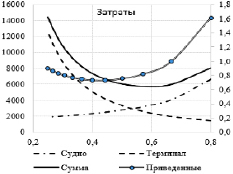
Рис. 2.3. Зависимость затрат в системе от загрузки терминала
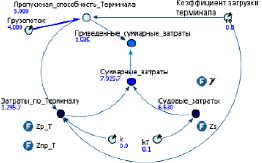
Рис. 2.4. Расчетная схема
Фрагмент результатов оптимизационного эксперимента, выполненного в среде AnyLogic, представлен на рис. 2.5. Видно, что приведенные суммарные затраты составляют 0,748 (УЕ/т), при этом интенсивность нагрузки терминала равна 0,44.
Рис. 2.5. Результаты решения оптимизационной задачи
Следует отметить, что дополнением к процедуре решения оптимизационных задач в среде AnyLogic выступает надстройка, позволяющая проводить параметрический анализ решения. Это дает возможность проанализировать влияние того или иного параметра на целевую функцию, выявить качественные и количественные закономерности этого влияния. В качестве примера на рис. 2.6 представлены результаты работы процедуры параметрического эксперимента – выявлена зависимость целевой функции задачи от интенсивности нагрузки терминала.
Рис. 2.6. Результат параметрического эксперимента
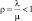
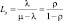
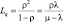
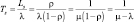
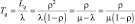
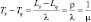
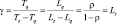
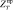