Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.3. Пример решения оптимизационной задачи
Произведем оптимизацию многоканальной системы с неограниченной очередью по критерию минимальных совокупных приведенных затрат в зависимости от количества причалов и интенсивности их нагрузки [5].
На рис. 2.8 приведена принципиальная схема моделируемой системы с элементами управления – интенсивностью входного потока, количеством причалов и средним временем обслуживания одного судна.
Рис. 2.8. Принципиальная схема СМО
Заготовка для простейшей 2-D анимационной схемы приведена на рис. 2.9.
Рис. 2.9. 2-D схема системы
При известном соотношении интенсивности потока судов и интенсивности их обслуживания (т.е. при заданной приведенной интенсивности потока судов, или интенсивности нагрузки терминала)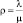 
задача сводится к определению оптимального числа задействованных причалов для обеспечения минимума целевой функции – совокупных приведенных затрат.
Формула расчета затрат по терминалу (2) преобразуется к виду:
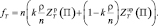
Соответственно изменится и вид целевой функции:
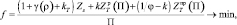
где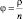 
– интенсивность нагрузки причалов.
Пусть П = 5000, ρ = 1,8, тогда минимальное количество задействованных причалов будет n = 2, при этом интенсивность их нагрузки составит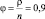 
.
В табл. 4 представлены результаты расчета показателей функционирования системы при различных (в диапазоне от 2 до 5) значениях количества задействованных причалов.
Таблица 4
Основные показатели работы СМО
|
Характеристики обслуживания |
Число причалов n |
|||
|
2 |
3 |
4 |
5 |
|
|
Вероятность простоя причалов p0 |
0,05 |
0,15 |
0,16 |
0,17 |
|
Средняя длина очереди Lq |
7,67 |
0,53 |
0,11 |
0,02 |
|
Затраты по судам fs |
6972 |
1814 |
1506 |
1446 |
|
Затраты по причалам fT |
1289 |
1839 |
2389 |
2939 |
|
Относительные затраты f |
1,65 |
0,73 |
0,78 |
0,88 |
Из данных, приведенных в табл. 4 следует, что необходимо задействовать 3 причала, при этом интенсивность нагрузки причалов составит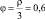 
.
На рис. 2.10 и 2.11 представлены основные характеристики работы системы, полученные во время моделирования в среде AnyLogic и соответствующие предельные значения, рассчитанные по формулам, приведенным в табл. 3.
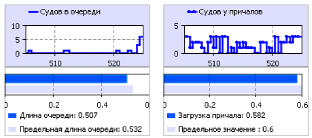
Рис. 2.10. Данные о длине очереди и загрузки причала
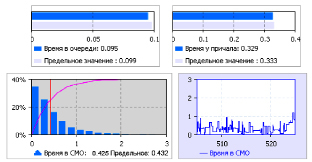
Рис. 2.11. Показатели времени в очереди, обслуживания и в системе
Процедура оптимизации в AnyLogic позволяет решать многопараметрические задачи. Так можно определить при каких сочетаниях приведенной интенсивности потока судов и числом задействованных причалов будет обеспечен минимум совокупных приведенных расходов. На рис. 2.12 представлен фрагмент поиска оптимума по двум параметрам – ρ и n.
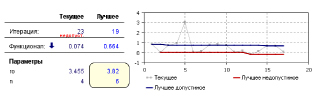
Рис. 2.12. Поиск оптимума по двум параметрам
Аналогично может выполняться оптимизация по любым другим параметрам и их комбинации.