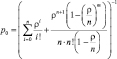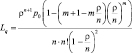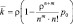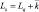Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.1.2. Многоканальные СМО
Рассмотрим n-канальную СМО с ожиданием, на которую поступает поток заявок с интенсивностью λ; интенсивность обслуживания m (для одного канала); число мест в очереди m.
Состояния системы нумеруются по числу заявок,находящихся в системе:
|
S0 |
– все каналы свободны |
|
S1 |
– занят один канал, остальные свободны |
|
… |
… |
|
Sk |
– заняты k-каналов, остальные свободны |
|
… |
… |
|
Sn |
– заняты все n-каналов, свободных нет |
|
S n+1 |
– заняты все n-каналов, одна заявка стоит в очереди |
|
… |
… |
|
S n+r |
– заняты все n-каналов, r-заявок в очереди |
|
… |
… |
|
S n+m |
– заняты все n-каналов, m-заявок в очереди |
Граф состояний многоканальной СМО с ограничением на длину очереди приведен на рис. 3.2 [5].

Рис. 3.2. Граф состояний многоканальной СМО при ограниченной длине очереди
У каждой стрелки проставлены соответствующие интенсивности потоков событий. Причем по стрелкам справа налево систему переводит поток обслуживаний интенсивность которого равна m, умноженному на число занятых каналов.
Очевидно в данном случае:
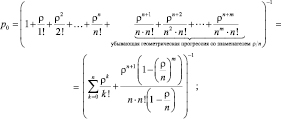
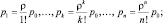
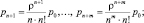
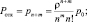
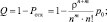
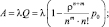
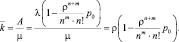
Среднее число заявок в очереди:
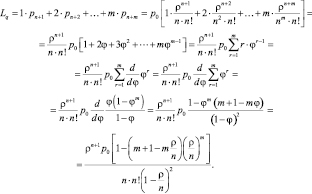
Среднее число заявок в системе:
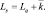
В табл. 5 приведены основные показатели работы СМО с ограниченной по длине очередью.
Таблица 5
Показатели работы многоканальной СМО с ограниченной очередью
|
№ п/п |
Наименование |
Формула |
|
|
1 |
p0 |
Вероятность того, что система находится в состоянии S0 |
|
|
2 |
Lq |
Среднее число заявок в очереди |
|
|
3 |
|
Среднее число заявок под обслуживанием (среднее число занятых каналов) |
|
|
4 |
Ls |
Среднее число заявок в системе |
|
|
5 |
Q |
Относительная пропускная способность |
|
|
6 |
A |
Абсолютная пропускная способность системы |
A = λQ |