Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.2. Результаты имитационного моделирования
Проведем имитационное моделирование и исследование вариантов описания потоков обслуживания и поступления заявок в соответствии с ранее сформулированными режимами. Пусть для примера интенсивности входящего потока заявок и потока обслуживаний имеют следующие значения: λ = 2, μ = 3 (в день).
1. Оба потока простейшие.
В данном случае предельная длина очереди и соответственно время ожидания в очереди составят:
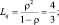
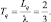
На рис. 5.2 представлен фрагмент моделирования потоков с информацией о длине очереди.

Рис. 5.2. Изменение длины очереди
Очевидно расчетная длина очереди в процессе имитации может отличаться от предельного значения. На рисунке представлен фрагмент времени, в течение которого расчётная длина являлась и больше и меньше своего предельного значения.
На рис. 5.3 приведена информация о среднем времени ожидания заявки в очереди и времени ее обслуживания.
2. Время обслуживания задается нечетким числом 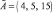 (часы).
(часы).
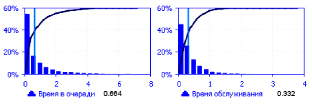
Рис. 5.3. Среднее время ожидания в очереди и обслуживания
Очевидно:
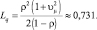
На рис. 5.4 представлен фрагмент имитационного моделирования с информацией о длине очереди. Длина очереди в данном случае меньше, чем в предыдущем случае, т.к. поток обслуживания ближе к регулярному.

Рис. 5.4. Графики изменения длины очереди
На рис. 5.5 приведены распределения для времени ожидания в очереди и времени обслуживания. Гистограмма для интервалов обслуживания качественно отличается от аналогичной, приведенной на рис. 5.3, где моделировался показательный закон распределения.
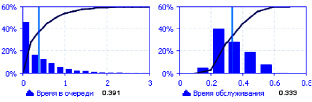
Рис. 5.5. Модельные значения времени обслуживания и обслуживания
3. Время обслуживания – константа, равная его математическому ожиданию (8 часов). Очевидно:
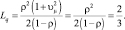
На рис. 5.6 и 5.7 представлены результаты моделирования для случая, когда время обслуживания постоянно. Очевидно, полученные данные близки по величине к варианту задания времени обслуживания в виде треугольного нечеткого числа.

Рис. 5.6. Данные о длине очереди
Предельная длина очереди в два раза меньше, чем для простейшего закона обслуживания, определяемого показательным законом распределения.
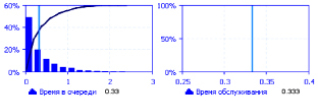
Рис. 5.7. Данные о времени проведенной заявкой в СМО
4. Оба потока описываются нечеткими числами.
Пусть время обслуживания задается нечетким числом 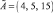 (часы), а для интервала времени между поступлением заявок используется нечеткое число
(часы), а для интервала времени между поступлением заявок используется нечеткое число 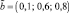 (дни).
(дни).
В этом случае:
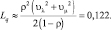
На рис. 5.8 и 5.9 представлены результаты имитационного эксперимента по моделированию СМО в условиях, когда в основу распределения времени обслуживания и интервалов времени поступления заявок, положены нечеткие числа.
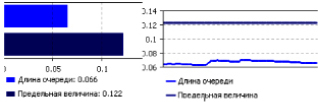
Рис. 5.8. Результаты моделирования по длине очереди
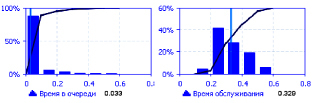
Рис. 5.9. Данные о времени обслуживания и ожидании в очереди
В данном случае расчетная длина очереди существенно меньше приближенной оценки ее предельной величины. Интервалы изменения возможных значений оценки длины очереди слева и справа, соответственно равны: