Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1. История вопроса
В начале прошлого века были проделаны эксперименты, результаты которых не укладывались в понятия классической физики и которые привели по существу к рождению квантовой физики. В квантовой механике было введено понятие волновой функции, которая непосредственно не имеет физического смысла, но, тем не менее, позволяет описать эволюцию квантовых систем во времени, а квадрат модуля волновой функции имеет смысл пространственно-временного распределения плотности вероятности этой системы.
Наибольшее число вопросов вызывает изложение квантовой механики инфинитного движения частиц. С какой бы общностью не пытались получить уравнение Шредингера [1, 2], все сводится к одному (по Шредингеру). Взято классическое выражение для энергии Е свободной частицы m, которая двигается с импульсом p
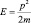(1.1)
и написано дифференциальное уравнение на языке плоских волн де Бройля для такого выражения.
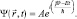(1.2)
В результате получается уравнение Шредингера для сводной частицы, которое с помощью волновой функции Ψ описывает её эволюцию в пространстве и времени.
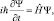(1.3)
где оператор Гамильтона для сводной частицы имеет вид:
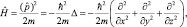
где ħ – постоянная Планка.
Уравнение Шредингера является комплексным, ему соответствуют два действительных уравнения. Волновая функция также является комплексной и, как уже говорилось, не имеет физического смысла. Физический смысл имеет плотность вероятности, собственно она описывает эволюцию частицы в пространстве и времени.
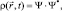(1.4)
где Ψ* – является комплексно сопряженной функцией.
И здесь возникает первое противоречие. Подставляя (1.2) в (1.4) получаем, что плотность вероятности свободной частицы постоянна во всем пространстве. Это необъяснимый факт. Получается что, плотность вероятности для свободной частицы, движущейся с импульсом 
, не зависит от координат и времени, то есть является постоянной во всем пространстве. Это противоречит экспериментальным данным. Попытка воспользоваться принципом суперпозиции и создать волновой пакет ни к чему не привела. Волновой пакет расплывается в пространстве и времени. В связи с этим один из современных способов решения квантовых задач инфинитного движения заключается в описании движения квантовых частиц с помощью огибающей волнового пакета на характерных размерах и временах много меньших чем параметры расплывания пакета.
Собственно с этого начинаются факты, лежащие в описании инфинитного движения в квантовой механике и не понятные до сих пор. На наш взгляд, одной из причин такого положения является то, что на заре зарождения квантовой механики отказались от описания квантовых систем с помощью физических величин. Это дорогая плата за введение нефизической функции Ψ. Дело в том, что при интерпретации квантовой механики в физических переменных без использования Ψ можно не только продвинуться в преодолении противоречий, имеющихся в квантовой механики, но и предсказать новые физические эффекты и экспериментально доказать их.
Как оказалось после публикации Э. Шредингером своего уравнения, на эту тему откликнулся Е. Маделунг и в 1926 году опубликовал уравнения движения квантовой частицы в физических переменных, которые имели квазигидродинамический вид. Одно из двух уравнений оказалось нелинейным. Раскопал всю эту библиографию Д. Бом, американский физик, который в 50-х годах внес значительный вклад в развитие квазигидродинамического описания квантовых систем [3, 4]. С тех пор нелинейный метод описания движения квантовых частиц с помощью величин, имеющих физический смысл, использовался для решения ряда квантовых задач. Например, при численных расчетах рассеяния квантовых частиц оказалось более удобным использовать квазигидродинамическое описание [5]. В конечном счете, использование квазигидродинамического описания оправдано, если получены новые результаты, которые подтверждаются экспериментально или могут иметь экспериментальное подтверждение.
Возможно, одной из причин того, что не «прижилось» квазигидродинамическое описание, является то, что одно из уравнений является нелинейным, которое весьма трудно решать аналитически. Впрочем, в квантовой механике не много решенных аналитически задач даже с использованием линейного уравнения Шредингера.
Поиск не тривиальных решений для инфинитных одночастичных состояний привел нас к решениям уравнения Шредингера в квазигидродинамическом виде. Квантовые квазигидродинамические уравнения позволяют описывать последовательно инфинитные и неинфинитные состояния квантовых частиц. При необходимости полученные результаты можно удостоверить с помощью традиционных решений уравнений Шредингера. Обращение к квантовым квазгидродинамическим уравнениям с физическими величинами позволяют несколько иначе взглянуть на давно известные результаты для одночастичных инфинитных состояний.
Описание квантовых систем с помощью квазигидродинамических уравнений будем называть представлением плотности вероятности и, как показывает опыт, квантовые задачи нужно решать в двух представлениях: с помощью волновых функций и с помощью представления плотности вероятности. Такой подход, в конечном счете, позволил предсказать существования субатомов водорода.
Литература
1. Д.И. Блохинцев. Основы квантовой механики. М.: Изд. Наука 1976. 664 с.
2. Л.Д. Ландау, Е.М. Лифшиц. Квантовая механика. Нерелятивистская теория. М.: Гиз. ФМЛ. 1963. 702 с.
3. Вопросы причинности в квантовой механике. Сб. переводов под ред. Я.П. Терлецкого и А.А. Гусева. М.: ИЛ 1955. С. 34.
4. Ghosh S.K., Deb B.M. Physics Reports (Review Section of Physics Letters). 92 № 1 (1982).
5. Б.В. Алексеев, А.И. Абакумов. Об одном подходе к решению уравнения Шредингера. Доклады Академии наук. Т. 262, С. 1100. 1982.