Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2. Полная энергия и волновая функция свободной частицы [2]
К сожалению, нередко в учебниках по квантовой механике выражением для полной энергии свободной частицы считается формула:
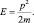(2.1)
Однако эта формула описывает только энергию поступательного движения частицы. Частица совершает одновременно ещё квантовое движение и это её неотъемлемое свойство, в каких бы она состояниях не находилась – финитных или инфинитных. Таким образом, свободная частица одновременно участвует в двух движениях («корпускулярно-волновой дуализм») и каждому движению должна соответствовать своя энергия.
Пусть оператор Гамильтона частицы массы m, совершающей свободное движение имеет вид:
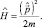(2.2)
В квантовой механике договорились и приняли, что реальной физической величине соответствует квантовомеханическое среднее от соответствующего оператора. Тогда энергия частицы равна:
(2.3)
Здесь принято:
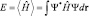и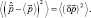 
Можно видеть, что квантовая частица одновременно участвует в двух движениях: совершая поступательное движение с кинетической энергией
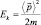
и чисто квантовое движение с энергией квантовой нелокальности движения, обусловленной флуктуациями импульса
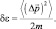
Таким образом,
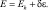(2.4)
Какой вид должна иметь волновая функция свободной частицы с энергией (2.4)? Используем принцип суперпозиции квантовых состояний для частицы, участвующей одновременно в двух движениях, и запишем волновую функцию в виде:
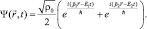(2.5)
Положим:
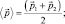
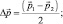
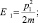
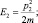
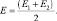
Обозначим далее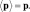 
Тогда плотность вероятности свободной частицы, совершающей инфинитное движение, будет иметь вид:
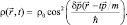(2.6)
Здесь предполагается, что начальная фаза волны равна нулю. Тогда один из максимумов плотности вероятности совпадает с классическим местоположением частицы, и этот центр перемещается в пространстве с импульсом 
. Использование большего числа волновых функций для написания суперпозиции, описывающей движение свободной частицы, приводит к известной проблеме – расплыванию ρ в пространстве со временем для каждой частицы. Принимая обозначения для полной энергии частицы Е и среднего импульса р волновую функцию частицы из формулы (2.5) можно преобразовать к виду:
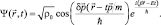(2.7)
Формула (2.7) показывает, что амплитуда плоской волны модулируется гармонической функцией и её максимум распространяется в пространстве с классической скоростью р/m. Период осцилляций амплитуды в пространстве подчиняется следующим соотношениям для любого момента времени:
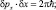
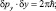
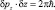
Не трудно убедиться, что подстановка волновой функции (2.7) в уравнение Шредингера для свободной частицы дает выражение для полной энергии частицы в виде формулы (2.3) или (2.4).
Далее покажем, что выражение для плотности вероятности свободной частицы (2.6) является аналитическим решением квантовых квазигидродинамических уравнений.
В общем случае волна плотности вероятности свободной частицы (2.6) совершает продольно-поперечные колебания с волновым вектором
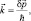(2.8)
частотой
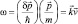(2.9)
и линейным законом дисперсии, что существенно. С её помощью качественно можно объяснить известные экспериментальные результаты по интерференции частицы самой с собой при прохождении двух щелей [1]. Заметим, что в монографии [1] при интерпретации интерференционной картины на экране предлагается суперпозиция двух волновых функций (после прохождения щелей) для описания инфинитного движения отдельной квантовой частицы.
Закон сохранения энергии движения для свободных частиц (2.4) с помощью (2.6) можно записать в следующем виде:
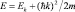или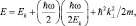 
(2.10)
где k^ – поперечна составляющая волнового вектора относительно направления движения. Можно видеть, что квантовая составляющая энергии свободного движения частицы имеет волновую природу и связана с энергией квантовых колебаний плотности вероятности. Заметим, что гармонические колебания плотности вероятности в соответствии с формулами (2.6) и (2.9) происходят на удвоенной частоте.
Если не учитывать поперечную составляющую флуктуаций импульса k^ = 0 и положить, что квантовая составляющая энергии движения равна кинетической энергии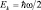 
, то получаем прежние постулаты квантовой механики для частиц с ненулевой массой.
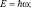
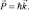
Эти формулы в соответствии с (2.10) описывают возможный частный случай.
Литература
1. Физика квантовой информации. Под ред. Д. Боумейстера, А. Экерта, А. Цайлингера. (М.: Постмаркет. 2002) с. 18. (The Physics of Quantum Information edited by D. Bouwmeester, A. Ekert, A. Zeilinger. Springer-Verlag Berlin Heidelberg 2000).
2. Неволин В.К. Об энергии движения свободных квантовых частиц в разреженных пучках. Журнал инженерная физика. 2009. № 5 С. 20.