Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
10. Энергия связи субатомных состояний водорода
Представление спина квантовых частиц как некого волнового движения с областью «темного» пространства в вероятностном центре распределения плотности вероятности позволило предложить идею субатома водорода, в котором в центре темного пространства электрона находится протон.
Предсказание субатомного состояния водорода весьма актуально для объяснения экспериментальных данных, полученных в области низкоэнергетических ядерных реакций [1–3].
Возможность существования субатомных состояний атома водорода покажем с помощью использования формулы де Бройля:
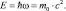(10.1)
Смысл этой формулы заключается в том, что элементарная частица с массой покоя m0 имеет собственную квантовую энергию движения, несвязанную с поступательным движением квантовой частицы.
Субатомные состояния атома водорода возможны тогда, когда расстояния между протоном и электроном настолько малы, что перекрываются области их пространственной локализации, вызванные наличием собственной квантовой энергии движения.
Уравнение для отыскания энергии связи системы, состоящей из электрона (индекс 1) и протона (индекс 2) запишется в виде:
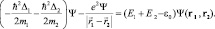(10.2)
Здесь E1 = m1c2, E2 = m2c2 – собственные энергии электрона и протона; ε0 – энергия связи субатома. Система координат расположена в центре распределения вероятности системы из двух частиц.
В уравнении (10.2) попробуем «выключить» вклад движения протона в полную энергию системы и свести задачу к одноэлектронному виду. Учтем, что масса протона существенно превосходит массу электрона m2 >> m1 и комптоновская длина электрона r10 много больше комптоновской длины протона
r20, r10 >> r20, (10.3)
где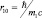 
и 
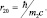
Это неравенство позволяет поместить начало координат в центре локализации протона, поскольку собственная пространственная область локализации протона значительно меньше области собственной локализации электрона. Тогда из (10.2) имеем:
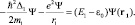(10.4)
Внешне уравнение (10.4) напоминает задачу о традиционном атоме водорода. Это одночастичное приближение для двухчастичной квантовой системы в нашем случае несколько ущербно и главное не учитывает наличия спина у протона и не может предсказать орто- и парасостояний субатомного водорода. В работе [4] сделана попытка решить это уравнение методом теории возмущений для случая E1 >> ε0. Такой подход вдохновлялся оценками энергии связи «нейтрония» (порядка 103 эВ) и экспериментальными данными, приведенными в работе [2]. При E1 >> ε0 решение уравнения (10.4) не может дать обычного квантования энергии связи ε0. Использование в первом прядке теории возмущения является достаточно грубым приближением. Волновые функции нулевого приближения представляют собой неоднородные стоячие волны, интегралы от которых расходятся [4]. В связи с этим проводилось обрезание интегралов для получения наибольшей величины энергии связи.
Заметим, что в работе [5] автор проводит аналитический расчет системы «электрон + протон» со скачкообразным потенциалом, состоящим из кулоновской энергии и положительной модельной постоянной потенциальной энергии. Наличие постоянной составляющей энергии в принципе соответствует нашей задаче. Однако в нашем случае положительная энергия строго определена и равна собственной энергии электрона m1c2, кроме того учитываются спиновые состояния электрона.
Для решения уравнения (10.4) используем сферическую систему координат и как обычно метод разделения переменных в задаче о падающей частице на силовой центр [6]. Представим Ψ(r, θ, φ) = R(r)Y(θ)Φ(φ), получим уравнения:
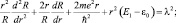(10.5)
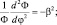(10.6)
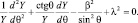(10.7)
Сначала решаем уравнение (10.6). Его решение запишем в виде отличном от [6]:
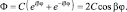(10.8)
Здесь учитывается тот факт, что оба вращательных направления равновероятны, в результате имеем колебательные состояния по углу φ, а условие однозначности будет выполняться для составляющей плотности вероятности
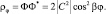(10.9)
В результате имеем более общий ряд квантования: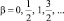 
Далее примем 
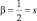– величина, равная спину электрона, которая не должна изменяться во внешних полях, в том числе в поле протона.
Найдем частное решение уравнения (10.7) для основного состояния в виде Y = sin θβ. Для констант разделения получим выражение λ2 = β(β + 1).
Для решения уравнения (10.5) введем безразмерную переменную
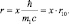
Получим:
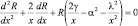(10.10)
где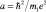 
– боровский радиус атом водорода, a >>> r10; 
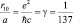– постоянная тонкой структуры;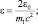 
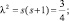α2 = ε – 2. Для свободной частицы ε = 0 и задача сводится к отысканию собственного волнового поля электрона. Такое поле вычислено аналитически в [4] и оно представляет собой радиальную стоячую неоднородную волну. Будем решать уравнение (10.10) в случае, когда ε > 2, полагая, что энергия связи должна превышать собственную энергию квантового движения электрона, чтобы удержать его в кулоновском поле протона. Это модель электронного облака, обусловленного собственной энергией движения электрона, в центре которого находится протон.
Решение будем искать в виде:
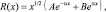(10.11)
где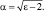 
В скобках опустим второе слагаемое, которое возрастает с увеличением координаты, и подставим искомое решение в уравнение (10.10). Получим:
2γ = 3α или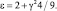 
Тогда энергия связи равна практически собственной энергии квантового движения электрона
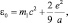(10.12)
где а – боровский радиус. Среднее расстояние электрона от протона определим как:
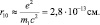
Область локализации протона оценим из соотношения:
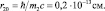
Величины областей локализации электрона и протона различаются более чем на порядок. Заметим, что область локализации свободного электрона за счет собственной энергии движения составляет 
что много меньше области локализации электрона в традиционном атоме водорода.
Таким образом, подтверждается исходная модель субатома водорода в виде облака электрона, обусловленная его собственной энергией движения, внутри которого находится протон. Полная энергия составляет ε0 ≈ 5∙105 эВ, что на два порядка больше, предсказываемой ранее [4]. При образовании таких атомов должно наблюдаться жесткое рентгеновское излучение. При столкновении электрона с протоном, электрон нужно затормозить в области локализации протона с характерными размерами менее 2,8∙10–13 см. Такая ситуация возможна при столкновении двух электронов в области локализации протона. При этом энергия одного из электронов должна соответствовать энергии связи субатома. Необходимо также наличие магнитного поля для ориентации спинов заряженных частиц. Напряжение, приложенное к разрядной трубке, может составлять при этом всего лишь несколько киловольт [2]. Полезно использовать магнитное поле и для торможения электронов относительно протонов до энергий равных энергии связи субатомов водорода.
Экспериментальное доказательство существования субатомов водорода послужит подтверждением справедливости соотношения де Бройля (10.1). Наконец, заметим, что это пока не совсем совершенное изложение идей субатома водорода и в последующих разделах оно будет уточнено.
Литература
1. C. Arata, Y-C. Zhang. Proceedings of the Japan Academy. Ser. B: Physical and Biological Sciences. 78, № 3, 57 (2002).
2. Ю.Л. Ратис. Журнал формирующихся направлений науки. 1, № 2, 27, (2013). http://www.unconv-science.org/n2.
3. С. Amsler. Particle data group. Phys. Lett. B. № 1. 667 (2008).
4. В.К. Неволин. Международный журнал прикладных и фундаментальных исследований. № 10 (ч. 5), 789, (2015). http://search.rae.ru.
5. V. Ignatovich. https://www.academia.edu/14205552/.
6. Ландау Л.Д. и Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. – М.: Физматлит. 1963. С. 130.