Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТРЕХМЕРНЫХ НЕСТАЦИОНАРНЫХ КОНВЕКТИВНЫХ ТЕЧЕНИЙ СЖИМАЕМОГО ВЯЗКОГО ТЕПЛОПРОВОДНОГО ГАЗА

Обухов А. Г., Сорокина Е. М.,

§5. Постановка краевых условий задачи возникновения и функционирования свободного теплового конвективного потока и их конечно-разностная аппроксимация

Ясно, что использование полной системы уравнений Навье – Стокса (4.1) добавляет трудностей (и математических, и вычислительных) по сравнению с использованием системы уравнений газовой динамики. Для этих двух систем по-разному задаются для компонент вектора скорости краевые условия на контактных поверхностях [95]. То есть на таких поверхностях, через которые сплошная среда не течет. Для системы уравнений газовой динамики на таких поверхностях предполагается равенство нулю нормальной составляющей к этой поверхности вектора скорости, а две остальные компоненты вектора скорости называются тангенциальными для данной поверхности (то есть лежат в касательной плоскости к ней) и их значения ничем не ограничиваются. Данное свойство называется «непротеканием». Для вязкой сплошной среды, течение которой описывается решениями полной системы уравнений Навье – Стокса (4.1), если по обе стороны от контактной поверхности заданы свои течения газа, то все компоненты векторов скорости на этой поверхности попарно совпадают – частицы среды этих двух течений на контактной поверхности как бы слипаются между собой из-за свойства вязкости. А если по вторую сторону от контактной поверхности течение среды не рассматривается, то на контактной поверхности равны нулю все три компоненты вектора скорости: и нормальная, и обе тангенциальные. Подобные условия обычно называются «условиями прилипания». Иногда область физического пространства, в которой рассматривается течение сплошной среды, ограничена. Однако не всегда границы такой области обусловлены физическими причинами. Часто положение границ определяется ограничениями на количество узлов разностной сетки, в которых численно строится решение. На таких поверхностях граничные условия задаются, исходя из условия непрерывности потока, далее называемые «условием непрерывности», или исходя из неизменности потока за пределами расчетной области – «условие симметрии». В первом случае краевые условия для искомых функций задаются с помощью интерполяции (как правило, линейной) значений функций из внутренней части расчетной области на ее границу. Во втором случае обычно на границе предполагается равенство нулю производных искомых функций в направлении нормали к граничной поверхности. Последнее условие часто несет и физический смысл. Например, для температуры оно означает теплоизолированность граничной поверхности.

Следует заметить, что в некоторых задачах постановка для полной системы уравнений Навье – Стокса на конкретных границах областей таких условий, какие задаются в случае невязкой нетеплопроводной среды, приводит в итоге к построению решений, которые соответствуют и газодинамическому (гидродинамическому) смыслу задачи и для которых выполняются законы сохранения.

Поскольку решения полной системы уравнений строятся численно для различных как по масштабам, так и по геометрической конфигурации областей, то предполагается, что расчетная область есть прямоугольный параллелепипед с длинами сторон x0, y0 и z0 вдоль осей Ox, Oy и Oz соответственно.

Граничные условия для всех функций, характеризующих сплошную среду, выбираются исходя из следующих условий.

Для плотности на всех шести гранях параллелепипеда: x = 0, x = x0, y = 0, y = y0, z = 0, z = z0 – предлагается ставить «условие непрерывности» потока, если других, имеющих содержательный физический смысл, условий задача не имеет. Это «условие непрерывности» потока означает, что значения искомой функции на границу области сносятся линейной интерполяцией по нормали к данной граничной поверхности из внутренней части расчетной области.

Краевые условия для компонент вектора скорости газа предлагается брать или соответствующими «условиям прилипания», или соответствующими «условиям непротекания» для невязкой среды для нормальной составляющей вектора скорости. Две другие компоненты вектора скорости течения подчиняются «условиям симметрии». А именно:

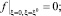
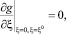(5.1)

где f – нормальная составляющая вектора скорости к поверхностям ξ = 0, ξ = ξ0, а g – две другие составляющие вектора скорости, то есть тангенциальные по отношению к поверхностям ξ = 0, ξ = ξ0.

Для температуры предлагается (если не оговорены какие-то другие конкретные условия) на всех гранях задавать условия теплоизоляции

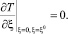(5.2)

А если, например, на плоскостях z = 0 и z = z0 значения температуры будут заданы, то именно они и должны быть взяты за краевые условия:

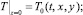
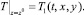(5.3)

Непосредственная разностная реализация предложенных краевых условий такова [95]. Расчетная область заполняется трехмерной сеткой узлов пересечения трех семейств плоскостей x = xi, y = yj, z = zk, где xi = i∙Δx, yj = j∙Δy, zk = k∙Δz, 0 ≤ i ≤ L, 0 ≤ j ≤ M, 0 ≤ k ≤ N. При этом 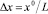, , 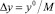 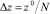– разностные шаги по трем пространственным переменным.

Пусть в начальный момент времени t = 0 во всех точках прямоугольного параллелепипеда все искомые функции заданы

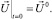(5.4)

Затем с помощью явной разностной схемы

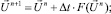
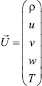(5.5)

вычисляются значения всех искомых функций во всех внутренних точках прямоугольного параллелепипеда. После этого значения искомых функций определяются во всех внутренних точках каждой из шести граней: x = 0, x = x0, y = 0, y = y0, z = 0, z = z0.

Если плотность на грани соответствует «условию непрерывности», то ее значения находятся с помощью линейной интерполяции по значениям плотности в двух точках, ближних по нормали к рассматриваемой грани (рис. 5.1 для граней z = 0, z = z0):

ρ(A) = 2ρ(B) – ρ(C). (5.6)

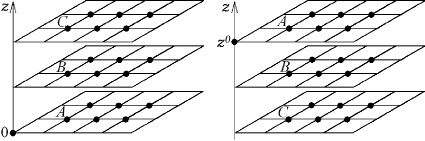
Рис. 5.1. Фрагменты расчетной сетки вблизи нижней поверхности z = 0
и верхней поверхности z = z0

Граничные условия для компонент вектора скорости задаются следующим образом. Компонента скорости вдоль оси Ox во внутренних точках граней x = 0, x = x0 принимается равной нулю. Во внутренних точках остальных четырех граней y = 0, y = y0, z = 0, z = z0 значения функции u определяются «по симметрии», то есть определяются из условия, что в этих точках производная по нормали к данной грани равна нулю (рис. 5.1 для граней z = 0, z = z0):

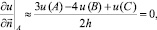(5.7)

откуда получается такая расчетная формула

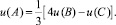(5.8)

Компонента скорости вдоль оси Oy во внутренних точках граней y = 0, y = y0 приравнивается нулю. Во внутренних точках остальных четырех граней x = 0, x = x0, z = 0, z = z0 значения функции v определяются «по симметрии», то есть определяются из условия, что в этих точках производная по нормали к данной грани равна нулю и, следовательно, получается такая расчетная формула (рис. 5.1 для граней z = 0, z = z0):

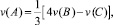(5.9)

что аналогично предыдущей формуле.

Компонента скорости вдоль оси Oz во внутренних точках граней z = 0, z = z0 полагается нулем. Во внутренних точках остальных четырех граней x = 0, x = x0, y = 0, y = y0 значения функции w определяются «по симметрии», то есть определяются из условия, что в этих точках производная по нормали к данной грани равна нулю и, следовательно, получается расчетная формула (рис. 5.2 для случаев граней x = 0, x = x0):

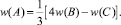(5.10)

Для температуры T во внутренних точках всех шести граней x = 0, x = x0, y = 0, y = y0, z = 0, z = z0 значения определяются «по симметрии» (для температуры – это «условие теплоизоляции»), то есть определяются из условия, что в этих точках производная по нормали к данной грани равна нулю:

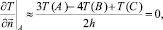(5.11)

и получается такая расчетная формула (рис. 5.1 для граней z = 0, z = z0):

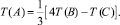(5.12)

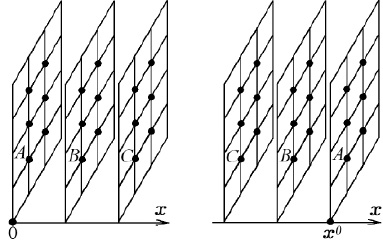
Рис. 5.2. Фрагменты расчетной сетки вблизи левой поверхности x = 0
и правой поверхности x = x0

В случае расчетов при заданных на плоскостях z = 0, z = z0 значениях температуры краевые условия считаются заданными, например:

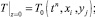
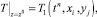(5.13)

где n – номер временного слоя и тогда t = Δt∙n.

Во внутренних точках остальных четырех граней x = 0, x = x0, y = 0, y = y0 значения температуры определяются «по симметрии» (для температуры – это условие «теплоизоляции»), то есть определяются из условия, что в этих точках производная по нормали к данной грани равна нулю и, следовательно, получается такая расчетная формула (рис. 5.2 для граней x = 0, x = x0):

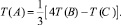(5.14)

Значения всех искомых функций во внутренних точках всех двенадцати ребер прямоугольного параллелепипеда вычисляется следующим образом (рис. 5.3).

На двух гранях, образующих ребро, берутся по две точки (B1C1), (B2C2), расположенные на нормалях к ребру, проведенных через рассматриваемую точку A. Затем вдоль каждой из этих нормалей линейной интерполяцией определяются два своих промежуточных значения искомой вектор-функции в точке A:

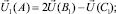
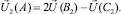(5.15)

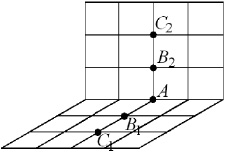
Рис. 5.3. Фрагмент расчетной сетки вблизи ребра

А затем значение на ребре в точке A берется как среднее арифметическое двух полученных промежуточных значений:

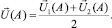(5.16)

В вершинах параллелепипеда значения вдоль каждого из трех ребер, приходящих в вершину, по двум ближайшим к вершине точкам линейной интерполяцией определяется свое промежуточное значение вдоль каждого ребра (рис. 5.4):

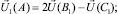
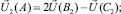
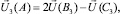(5.17)

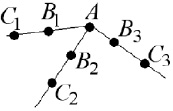
Рис. 5.4. Фрагмент расчетной сетки вблизи вершины

а затем значение в вершине берется как среднее арифметическое трех полученных значений:

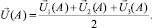(5.18)

В задаче численного моделирования возникающих сложных конвективных течений воздуха над нагревающейся областью поверхности Земли предлагается рассматривать расчетную область в виде прямоугольного параллелепипеда (рис. 5.5). Его нижняя грань, совпадающая с поверхностью Земли, имеет форму квадрата со стороной, равной безразмерному единичному масштабному значению расстояния (размерное значение 100 км). Высота имеет безразмерное значение 0,1 (размерное значение 10 км). Размеры расчетной области в данном случае приняты такими, чтобы максимально приблизить их к размерам возникающих конвективных потоков в атмосфере Земли при формировании, например, тропических циклонов.

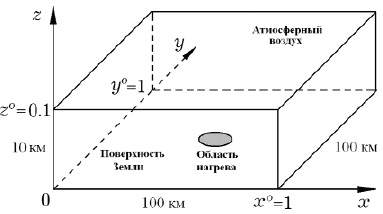
Рис. 5.5. Расчетная область в виде прямоугольного параллелепипеда

Начальные условия задаются с помощью соотношений (4.11)–(4.13). При этом набор из пяти указанных функций, являющихся точным аналитическим решением полной системы уравнений Навье – Стокса в бесконечном физическом полупространстве, используется в качестве начальных условий при численном моделировании конвективных течений сжимаемого вязкого теплопроводного газа для ограниченного пространства выбранной расчетной области.

Исходя из физических соображений, для рассматриваемой задачи поставлены следующие конкретные граничные условия.

Для плотности на всех шести гранях расчетного параллелепипеда x = 0, x = x0, y = 0, y = y0, z = 0, z = z0 ставится «условие непрерывности», при котором значения плотности на границу области сносятся линейной интерполяцией из внутренней части расчетной области. Это означает, что в процессе расчетов плотность воздуха может изменяться на всех гранях расчетного параллелепипеда в соответствии с установленными в полной системе уравнений Навье – Стокса закономерностями.

Нормальные составляющие вектора скорости на нижней и верхней грани z = 0, z = z0 берутся равными нулю 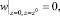а для двух других (тангенциальных) компонент вектора скорости на нижней и верхней гранях z = 0, z = z0 ставятся «условия непрерывности» и для этих граней (рис. 5.1) тангенциальные компоненты скорости газа рассчитывается по формулам

u(A) = 2u(B) – u(C); v(A) = 2v(B) – v(C).

Это означает, что воздух не может пересекать нижнюю и верхнюю граничные поверхности расчетной области, но может двигаться вдоль них.

Все компоненты вектора скорости на четырех боковых гранях рассчитываются из «условия непрерывности». Это означает, что воздух может пересекать все боковые граничные поверхности расчетной области. Например, расчетные формулы для компонент скоростей для случаев граней x = 0, x = x0 (рис. 5.2) имеют вид

u(A) = 2u(B) – u(C); v(A) = 2v(B) – v(C); w(A) = 2w(B) – w(C).

Для температуры на пяти гранях, кроме нижней, задаются «условия теплоизоляции», при которых производная от температуры в направлении нормали к соответствующей грани равна нулю. Например, для верхней грани z = z0 (рис. 5.6)

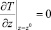или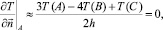

откуда получается такая расчетная формула

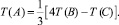
Другими словами, внутренняя часть расчетной области не обменивается теплом с окружающим пространством.

Рис. 5.6. Фрагмент расчетной сетки вблизи верхней поверхности z = z0

Температуру на плоскости z = 0 предлагается задавать функцией

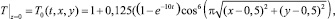
моделирующей локальный круговой нагрев солнечной энергией поверхности Земли (рис. 5.7). В этой формуле фоновое значение температуры равно масштабной единице (размерное значение 288 °К = 15 °С), коэффициент 0,125 (размерное значение 36°) равен превышению максимальной температуры нагрева над фоновой температурой и задается в качестве входного значения в разных вариантах расчета. Множитель (1 – e–10t) обеспечивает плавное нарастание температуры нагрева от фонового до максимального значения. Таким образом, максимум нагрева на рис. 5.7 соответствует температуре 51 °С.

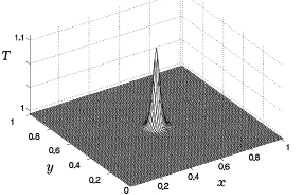
Рис. 5.7. Распределение температуры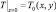
в момент достижения ею своего максимального значения

Выбор в таком виде граничных условий с одной стороны наиболее адекватен физической сущности природных явлений конвекции атмосферного воздуха, а с другой стороны позволяет организовать процедуру численного построения решения полной системы уравнений Навье – Стокса для моделирования трехмерных нестационарных конвективных течений атмосферного воздуха и обеспечить устойчивость вычислительной схемы.

В задаче численного моделирования возникающих сложных конвективных течений воздуха над нагревающейся нижней поверхностью контейнера рассматривается в расчетной области в виде куба (рис. 5.8). Его нижняя грань, совпадающая с поверхностью Земли, имеет форму квадрата со стороной, равной единичному масштабному значению расстояния (размерное значение 10 м).

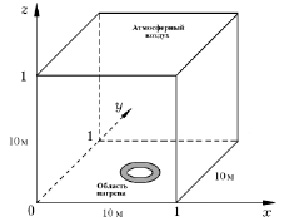
Рис. 5.8. Расчетная область в виде куба

Начальные условия для моделирования этой задачи выбираются такими же, как в первой задаче (за исключением масштабного размерного значения расстояния 10 м).

Граничные условия для моделирования рассматриваемой задачи предлагаются следующие.

Для плотности на всех шести гранях расчетного куба ставится «условие непрерывности», при котором значения плотности на границу области сносятся линейной интерполяцией из внутренней части расчетной области. Это означает, что в процессе расчетов плотность воздуха может изменяться на всех гранях расчетного куба в соответствии с установленными в полной системе уравнений Навье – Стокса закономерностями. Например, для нижней и верхней грани z = 0, z = z0 (рис. 5.1) плотность газа рассчитывается по формуле

ρ(A) = 2ρ(B) – ρ(C).

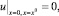
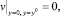
Для нормальных составляющих вектора скорости ко всем граничным поверхностям берутся равными нулю 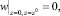а для двух других (тангенциальных) компонент вектора скорости ко всем граничным поверхностям ставятся «условия симметрии». Это означает, что воздух не может пересекать граничные поверхности расчетной области, но может двигаться вдоль них. «Условия симметрии» означают, что производные от тангенциальных компонент вектора скорости в направлении нормали к соответствующей грани равны нулю. Например, для верхней грани z = z0 (рис. 5.6)

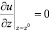или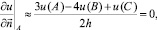

откуда получается расчетная формула

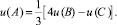
Для температуры на пяти гранях кроме нижней задаются «условия теплоизоляции», при которых производная от температуры в направлении нормали к соответствующей грани равна нулю. Другими словами, внутренняя часть расчетной области не обменивается теплом с окружающим пространством.

Для рассматриваемой задачи температура на плоскости z = 0 в кольце между концентрическими окружностями с безразмерными значениями радиусов 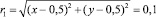и 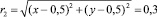 задана в виде функции

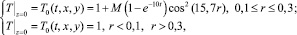
моделирующей кольцеобразный локальный нагрев нижней грани расчетного куба (рис. 5.8). Задаваемый коэффициент M в последней формуле определяет максимальное значение температуры нагрева в разных вариантах расчета и равен разности между максимальным безразмерным значением температуры локального нагрева и масштабным безразмерным значением температуры M = Tmax – 1.

Задание функции нагрева нижней поверхности расчетной области в представленном виде определено тем, что во многих технических устройствах нагревательные элементы имеют форму спирали, или форму одного или нескольких колец. Поэтому моделирование такого вида нагревательных элементов представляет практический интерес.