Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Обухов А. Г., Сорокина Е. М.,
§6. Конечно-разностная аппроксимация полной системы уравнений Навье – Стокса
Как уже отмечалось, расчетная область в виде прямоугольного параллелепипеда заполняется трехмерной сеткой узлов пересечения трех семейств плоскостей, определяющих разностные шаги по трем пространственным переменным. Фрагмент трехмерной расчетной сетки узлов изображен на рис. 6.1.
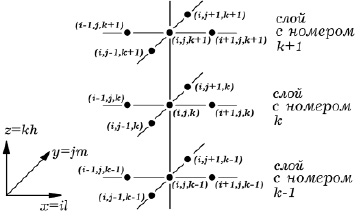
Рис. 6.1. Фрагмент трехмерной расчетной сетки узлов
По известным в начальный момент времени искомым функциям с помощью явной разностной схемы вычисляются значения искомых функций во внутренних точках прямоугольного параллелепипеда. Данная вычислительная процедура для первого уравнения системы (4.1), записанного в скалярном виде
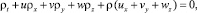(6.1)
представляется следующим образом. Воспользовавшись для аппроксимации производной по времени значениями функции плотности с двух последовательных временных слоев в узле (i, j, k)
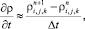(6.2)
а для аппроксимации производных по пространственным переменным центральные разности значений функций (рис. 6.1)
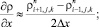
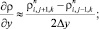
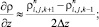(6.3)
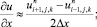
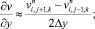
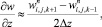(6.4)
перепишем уравнение (6.1) в виде:
(6.5)
Отсюда получим разностное уравнение для вычисления плотности газа во внутреннем узле (i, j, k) расчетной области
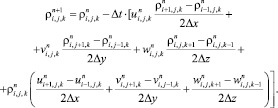(6.6)
Аналогично для второго уравнения системы (4.1) в скалярном виде
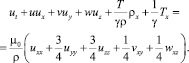(6.7)
Аппроксимируя производную по времени значениями функции скорости u с двух последовательных временных слоев в узле (i, j, k)
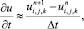(6.8)
а для аппроксимации производных по пространственным переменным центральные разности значений функций
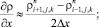
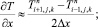(6.9)
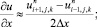
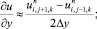
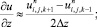(6.10)
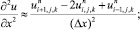
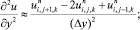(6.11)
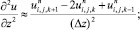(6.12)
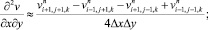(6.13)
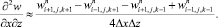(6.14)
Перепишем уравнение (6.7) в виде:
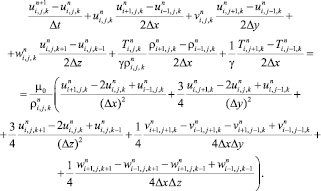(6.15)
Отсюда получим разностное уравнение для вычисления первой компоненты скорости u во внутреннем узле (i, j, k) расчетной области
(6.16)
Для третьего уравнения системы (4.1), записанного в скалярном виде
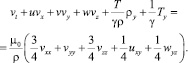(6.17)
Аппроксимируя производную по времени значениями функции скорости v с двух последовательных временных слоев в узле (i, j, k)
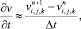(6.18)
а для аппроксимации производных по пространственным переменным центральные разности значений функций (рис. 6.1)
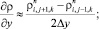
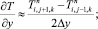(6.19)
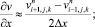
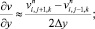
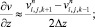(6.20)
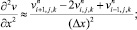
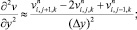(6.21)
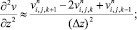(6.22)
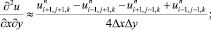(6.23)
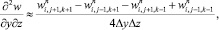(6.24)
перепишем уравнение (6.17) в виде:
(6.25)
Отсюда получим разностное уравнение для вычисления второй компоненты скорости v во внутреннем узле (i, j, k) расчетной области
(6.26)
Для четвертого уравнения системы (4.1), записанного в скалярном виде
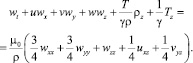(6.27)
Аппроксимируя производную по времени значениями функции скорости w с двух последовательных временных слоев в узле (i, j, k)
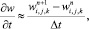(6.28)
а для аппроксимации производных по пространственным переменным используя центральные разности значений функций (рис. 6.1)
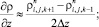
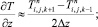(6.29)
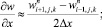
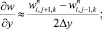
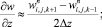(6.30)
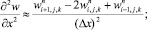
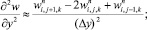(6.31)
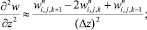(6.32)
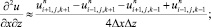(6.33)
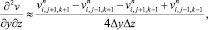(6.34)
перепишем уравнение (6.27) в виде:
(6.35)
Отсюда получим разностное уравнение для вычисления третьей компоненты скорости w во внутреннем узле (i, j, k) расчетной области
(6.36)
И, наконец, для пятого уравнения системы (4.1), записанного в скалярном виде
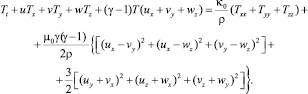(6.37)
Аппроксимируя производную по времени значениями функции температуры T с двух последовательных временных слоев в узле (i, j, k)
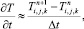(6.38)
а для аппроксимации производных по пространственным переменным используя центральные разности значений функций
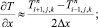
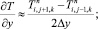
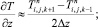(6.39)
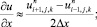
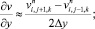
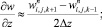(6.40)
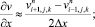
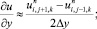
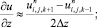(6.41)
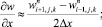
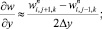
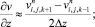(6.42)
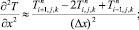
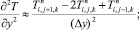(6.43)
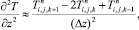(6.44)
перепишем уравнение (6.37) в виде:
(6.45)
Получим разностное уравнение для вычисления температуры T во внутреннем узле (i, j, k) расчетной области
(6.46)
Полученные выше соотношения (6.6), (6.16), (6.26), (6.36), (6.46) являются конечно-разностными уравнениями полной системы уравнений Навье – Стокса для численного расчета всех газодинамических функций n + 1 временного слоя во всех внутренних узлах расчетной области в тройном вложенном цикле по трем пространственным переменным. После этого, используя граничные условия, значения искомых функций рассчитываются во всех точках граней, ребер и вершин расчетной области. Алгоритм расчета подробно описан в пятом параграфе.