Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.3. Многоальтернативная проверка гипотез
Рассмотрим процедуру принятия решения при наличии нескольких вариантов: изображения нескольких классов, кодовые комбинации, соответствующие нескольким передаваемым сигналам, дактилоскопические исследования группы людей, распознавание букв русского алфавита и т.п.
Итак, предположим, что имеется М 2 альтернатив, причем каждой из них априори приписывают некоторую стоимость и полагают, что задана система априорных вероятностей Р0, Р1,…, РМ–1 для каждой из М возможных гипотез.
Для отыскания байесовского правила решения обозначим названную выше стоимость каждого образа действий через Сij (i-я гипотеза выбрана в качестве истинной, а j-я гипотеза является истинной на самом деле).
Область пространства, в которой мы выбираем гипотезу Hi, обозначим Гi.
Запишем выражение для риска:
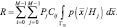
Решение будет оптимальным при таком разбиении пространства Г на М непересекающихся подпространств, чтобы риск был минимален.
Метод решения данной задачи не отличается от предыдущего. Проиллюстрируем обобщение для М = 3.
Поскольку области не пересекаются, постольку Г0 = Г – Г1 – Г2. Запишем выражение для риска.
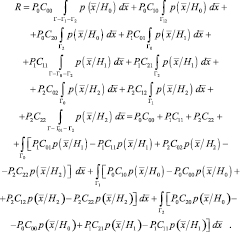 (2.3.1)
(2.3.1)
После несложных преобразований получим
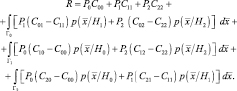
Решение принимается в пользу той гипотезы, для которой соответствующее подынтегральное выражение в формуле (2.3.1) меньше:
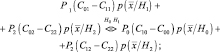
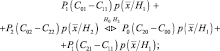 (2.3.2)
(2.3.2)
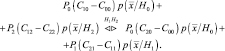
Определим отношение:
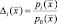 (2.3.3)
(2.3.3)
и перепишем правило решения (2.3.3) в виде:
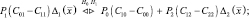
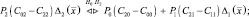
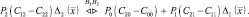
Рассмотрим частный случай, когда стоимости ошибочных решений одинаковы и равны единице, а стоимости верных решений считаются равными нулю:
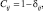 (2.3.4)
(2.3.4)
где ?ij – символ Кронекера,
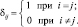
При этом получаем простое правило решения:
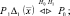
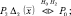
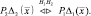
Подставляя (2.3.3) в (2.3.4), приходим к следующему правилу решения:
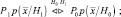
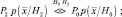
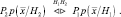
В этом случае оптимальный критерий классификации заключается в формировании апостериорной плотности вероятности для каждого возможного класса и выбора максимума.
Обобщение на случай произвольного числа классов М очевидно.
Решение о выборе номера класса производится путем отыскания максимума апостериорной плотности: