Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.4. Случай многих классов
Канонической формой классификатора может служить его представление в виде системы разделяющих функций 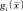 . Классификатор ставит вектор признаков
. Классификатор ставит вектор признаков  в соответствие гипотезе (классу) Hi, если для всех j ≠ i справедливо неравенство
в соответствие гипотезе (классу) Hi, если для всех j ≠ i справедливо неравенство
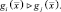
Классификатор, таким образом, рассматривается как устройство, вычисляющее М разделяющих функций и выбирающее решение, соответствующее наибольшей из них.
Очевидно, что выбор разделяющих функций не единственен. Всегда можно, не влияя на решение, умножить разделяющие функции на положительную константу или прибавить к ним какую-либо константу. Более того, если заменить каждую из 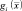 на
на 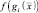 , где f(•) – монотонно возрастающая функция, то результат классификации не изменится. Это обстоятельство может привести к существенным аналитическим и расчетным упрощениям. В частности, при классификации с минимальным уровнем наиболее удобным на практике вариантом разделяющей функции является
, где f(•) – монотонно возрастающая функция, то результат классификации не изменится. Это обстоятельство может привести к существенным аналитическим и расчетным упрощениям. В частности, при классификации с минимальным уровнем наиболее удобным на практике вариантом разделяющей функции является
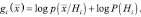 (2.4.1)
(2.4.1)
Решающие правила остаются эквивалентными. Действие решающего правила заключается в разбиении пространства признаков  на М областей решений Г1, Г2, …, ГМ. Уравнение границы, разделяющей области Гi и Гj имеет вид
на М областей решений Г1, Г2, …, ГМ. Уравнение границы, разделяющей области Гi и Гj имеет вид