Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОПТИМАЛЬНАЯ ОБРАБОТКА РАДИОЛОКАЦИОННЫХ ИЗОБРАЖЕНИЙ, ФОРМИРУЕМЫХ В РСА

Доросинский Л. Г.,

2.5. Вероятности ошибок и интегралы ошибок

Рассмотрим случай двух классов. Возможно два типа ошибок классификации:

• вектор наблюдаемых данных попадает в пространство Г₁ в то время, как истинное состояние природы соответствует гипотезе Н₀;
• вектор наблюдаемых данных попадает в пространство Г₀, хотя истинное состояние природы – Н₁.

В связи с тем, что названные события взаимоисключающие и составляют полное множество событий, вероятность ошибки может быть рассчитана в соответствии с выражением

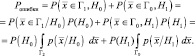
В случае многих классов проще вычислить вероятность правильного решения:

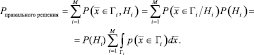
Полученный результат справедлив при любом разбиении пространства решений. Разбиение в соответствии с байесовским критерием гарантирует, что полученная вероятность будет максимальной.