Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОПТИМАЛЬНАЯ ОБРАБОТКА РАДИОЛОКАЦИОННЫХ ИЗОБРАЖЕНИЙ, ФОРМИРУЕМЫХ В РСА

Доросинский Л. Г.,

2.8. Байесовский классификатор

Из курса математической статистики известно, что оценка по максимуму правдоподобия для ковариационной матрицы смещена, т.е. ожидаемое значение не равно R. Несмещенная оценка для R задается выборочной ковариационной матрицей

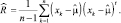(2.8.1)

Очевидно, что оценки (2.7.3) и (2.8.1), совпадают при большом n.

Наличие двух сходных и тем не менее разных оценок для ковариационной матрицы смущает многих исследователей, т.к. возникает вопрос: какая же из них «верная»? Ответить на это можно, сказав, что каждая из этих оценок ни верна, ни ложна: они просто различны. Наличие двух различных оценок показывает, что единой оценки, включающей все свойства, которые только можно пожелать, не существует. Для наших целей сформулировать наиболее желательные свойства довольно сложно – нам нужна такая оценка, которая позволила бы наилучшим образом проводить классификацию. Хотя разрабатывать классификатор, используя оценки по максимуму правдоподобия для неизвестных параметров, обычно представляется разумным и логичным, вполне естествен вопрос, а нет ли других оценок, обеспечивающих еще лучшее качество работы. В данном разделе мы рассмотрим этот вопрос с байесовской точки зрения.

Сущность байесовской классификации заложена в расчете апостериорной вероятности 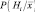. Байесовское правило позволяет вычислить эти вероятности по априорным вероятностям P(Hi) и условным по классу вероятностям 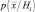. Однако возникает вопрос: как быть, если названные вероятности неизвестны. Для ответа на него мы должны вычислить 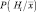, максимально используя всю информацию, которая есть в нашем распоряжении. Часть такой информации может быть априорной, часть содержаться в множестве выборок. Пусть X означает множество выборок. Применив формулу Байеса, получим апостериорную плотность вероятности

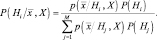(2.8.2)

В данном выражения мы считаем, что значения априорных вероятностей известны и не зависят от выборок X. Кроме того, предполагаем, что выборки можно разделить по классам на М подмножеств: X1, X2, …, XM, причем выборки Xi принадлежат Hi. и не оказывают влияния на все 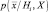, если i ≠ j. Принятые предположения позволяют записать уравнение (2.8.2) в виде

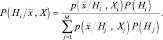(2.8.3)

Для принятия решения по правилу (2.8.3), например, путем выбора максимума, мы должны решить М задач оценки M плотностей вероятностей 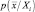по M обучающим выборкам.

Для примера решим задачу оценки неизвестного вектора средних значений . Начнем анализ с одномерного случая, когда p(x/μ) представляет собой нормальное распределение с математическим ожиданием, равным m и дисперсией σ² и общее число выборок равно n: X = {x₁, x₂, …, x_n}.

Предположим, что априорные сведения о среднем значении m исчерпываются известной априорной плотностью, которая также считается нормальной с математическим ожиданием µ₀ и дисперсией .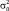

Для определения среднего значения воспользуемся байесовским правилом. Апостериорная плотность параметра имеет вид

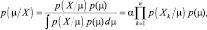(2.8.4)

где a – масштабный множитель, не зависящий от m.

Подставляя в выражение (2.8.4) соответствующие нормальные плотности вероятностей, получаем:

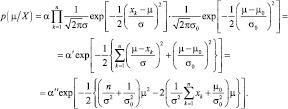(2.8.5)

В выражении (2.8.5) множители, не зависящие от m, включены в константы α′ и α″.

Из (2.8.5) также следует, что плотность p(μ/X) является нормальной. Обозначим параметры полученной нормальной плотности, как μ_n и σ²_n, которые могут быть получены приравниваем коэффициентов из выражения (2.8.5) соответствующим коэффициентам из выражения

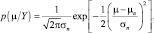
Отсюда получаем:

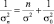и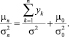

Решая уравнения в явном виде, получаем

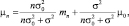(2.8.6)

где m_n – выборочное среднее;

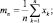
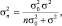
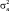– выборочная дисперсия.

Из уравнения (2.8.6) видно, что оптимальная оценка математического ожидания апостериорной плотности представляет собой линейную комбинацию априорного математического ожидания µ0 и выборочного среднего m_n, полученного по n выборкам. Коэффициенты перед этими величинами неотрицательны и в сумме равны единице.

Если достоверность априорных данных очень высока 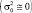, то в качестве оценки следует использовать априорное математическое ожидание µ₀. Это говорит о том, что никакое число измерений не может поколебать нас в уверенности в априорных данных.

При альтернативной ситуации (σ²₀ ≠0, а число наблюдений стремится к бесконечности: n > ?, 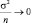) в качестве оценки следует использовать выборочное среднее mn, не доверяя, в свою очередь, априорным сведениям. Вообще относительный баланс между априорными представлениями и опытными данными определяется отношением σ² к σ²₀, называемым иногда догматизмом. Если догматизм не бесконечен, то после получения достаточного числа выборок априорные данные перестают играть сколько-нибудь заметную роль, а оценка стремится к выборочному среднему.

После получения апостериорной плотности p(μ/X) остается определить «условную по классу» плотность p(x/X) (в данном выводе мы полагаем, что все выборки принадлежат одному, например, j-му классу с априорной плотностью p(H_j)). Для определения требуемой плотности вычислим

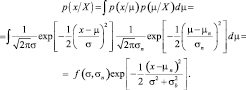
Отсюда следует, что плотность 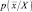является нормальной со средним значением, равным µn, и дисперсией .

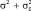Для получения байесовского решения полученную плотность для каждого j-го класса следует умножить на априорную вероятность этого класса и выбрать максимальное значение