
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.9. Эффективность оценки. Нижняя граница дисперсии несмещенной оценки. Неравенство Крамера-Рао
Предположим, что мы производим оценку неизвестного неслучайного параметра Θ и в результате измерений получаем так называемую несмещенную оценку, т.е. такую оценку, математическое ожидание которой равняется значению самого оцениваемого параметра, т.е. 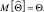 Для того чтобы определить качество оценки, следует определить ее дисперсию, которая вычисляется следующим образом:
Для того чтобы определить качество оценки, следует определить ее дисперсию, которая вычисляется следующим образом:
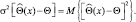
Дисперсия дает меру рассеяния ошибки. Наилучшей оценкой была бы, по-видимому, несмещенная оценка с минимальной дисперсией. Однако регулярной процедуры, которая бы приводила к получению алгоритма, формирующего несмещенную оценку с минимально возможной дисперсией, не существует.
В этой ситуации имеет смысл получить выражение для нижней границы дисперсии любой несмещенной оценки. Знание границы позволит сравнить дисперсию той или иной оценки с этой границей, и в том случае, если будет получено совпадение дисперсии оценки с нижней границей, может быть сделан вывод, что мы получили наилучшую оценку. Если же точное совпадение не обеспечено, то и в этом случае мы можем судить, насколько наша оценка отличается от потенциально достижимой.
Докажем следующее утверждение. Если 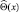 – любая несмещенная оценка величины Θ, то
– любая несмещенная оценка величины Θ, то
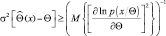 (2.9.1)
(2.9.1)
или, что эквивалентно,
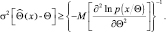 (2.9.2)
(2.9.2)
При этом мы считаем, что производные
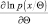 и
и 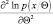
существуют и являются абсолютно интегрируемы.
Неравенства (2.9.1) и (2.9.2) обычно называются границами Крамера-Рао. Любая оценка, удовлетворяющая указанной границе со знаком равенства, называется эффективной оценкой.
Доказательство этого положения основано на использовании неравенства Буняковского-Шварца. Так как по нашему предположению оценка считается несмещенной, запишем
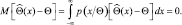 (2.9.3)
(2.9.3)
Дифференцируя обе части по Θ, имеем
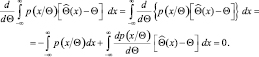 (2.9.4)
(2.9.4)
Первый интеграл равен 1. Кроме того, заметим, что
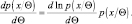 (2.9.5)
(2.9.5)
Подставляя (2.9.5) в (2.9.4), получаем
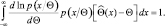
Перепишем подынтегральное выражение в следующем виде:
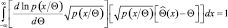
и используем неравенство Буняковского-Шварца:
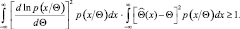 (2.9.6)
(2.9.6)
В связи с тем, что каждый из сомножителей представляет собой математическое ожидание, имеем следующее неравенство:
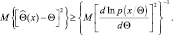
Итак, неравенство (2.9.1) можно считать доказанным. Для доказательства неравенства (2.9.2) заметим, что
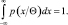
Дифференцируя по Θ, имеем
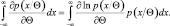 (2.9.7)
(2.9.7)
Вновь дифференцируя по Θ и применяя (2.9.5), получим
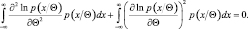
Отсюда следует
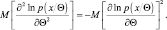
Последнее равенство означает справедливость условия (2.9.2).
Неравенство Крамера-Рао позволяет сделать ряд важных замечаний.
1. Любая несмещенная оценка имеет дисперсию больше, чем некоторое число.
2. Неравенство Буняковского-Шварца (2.9.6) выполняется тогда и только тогда, когда
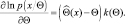 (2.9.8)
(2.9.8)
Если эффективная оценка существует (равенство (2.9.8) выполняется), то эта оценка является оценкой максимального правдоподобия. Действительно, уравнение правдоподобия имеет вид
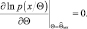
Для того чтобы правая часть равенства (2.9.8) принимала нулевое значение, оценка  должна быть равна
должна быть равна  .
.
3. Если эффективной оценки не существует (равенство (2.9.8) не выполняется), то неизвестно, насколько оптимальной является оценка максимального правдоподобия (насколько близко она приближается к границе). В этой ситуации границу и дисперсию оценки приходится вычислять и полученные величины сравнивать. Однако достаточно обнадеживающим является тот факт, что оценка по максимуму правдоподобия является асимптотически эффективной, иначе говоря, при стремлении размера выборки (размерности вектора x к бесконечности) дисперсия оценки максимального правдоподобия стремится к своей границе.
