
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.10.1. Оценка плотности распределения
Методы оценки неизвестной плотности распределения основываются на том, что вероятность P попадания вектора x в область R задается выражением:
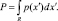 (2.10.1)
(2.10.1)
Таким образом, Р есть усредненный вариант плотности распределения р(x), и можно оценить это значение р посредством оценки вероятности Р. Предположим, что n выборок x1, x2, …, xn берутся независимо друг от друга в соответствии с вероятностным законом р(x). Очевидно, что вероятность попадания k из n выборок в R задается биномиальным законом
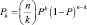 (2.10.2)
(2.10.2)
и ожидаемой величиной k будет
E[k] = nP. (2.10.3)
Более того, это биномиальное распределение для k имеет довольно резко выраженные максимумы около среднего значения, поэтому мы считаем, что отношение k/n будет хорошей оценкой вероятности Р, а следовательно, и сглаженной плотности распределения. Если теперь мы допустим, что р(x) непрерывна и область R настолько мала, что р в ее пределах меняется незначительно, то можем написать
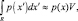 (2.10.4)
(2.10.4)
где х – это точка внутри R и V – объем R. Объединяя уравнения (2.10.1)–(2.10.4), получаем следующую очевидную оценку для р(x):
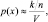
Остается решить несколько проблем практического и теоретического плана. Если мы фиксируем объем V и делаем все больше и больше выборок, отношение k/n сойдется (по вероятности) требуемым образом, но при этом мы получаем оценку только пространственно усредненной величины р(x):
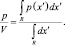
Если мы хотим получить р(x), а не усредненный ее вариант, необходимо устремить V к нулю. Однако если зафиксировать количество n выборок и позволить V стремиться к нулю, то область в конечном счете станет настолько мала, что не будет содержать в себе никаких выборок, и наша оценка р(x) @ 0 будет бесполезной.
С практической точки зрения количество выборок всегда ограничено, так что нельзя позволить объему V становиться бесконечно малым. Если приходится пользоваться таким видом оценки, то нужно допускать определенную дисперсию отношения k/n и определенное усреднение плотности распределения р(x).
С теоретической точки зрения интересно, как можно обойти эти ограничения при наличии неограниченного количества выборок. Предположим, что мы пользуемся следующей процедурой. Для оценки плотности распределения x мы образуем последовательность областей, содержащих x. Первая область будет соответствовать одной выборке, вторая – двум и т.д. Пусть Vn будет иметь объем Rn, kn – количество выборок, попадающих в Rn, а pn(x) – n-я оценка р(x):
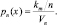 (2.10.5)
(2.10.5)
Если рn(x) должна сойтись к р(x), то следует выполнить три условия:
1. 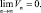
2. 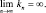
3. 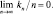
Первое условие обеспечивает сходимость пространственно усредненного P/V к р(x) при однородном сокращении областей и при непрерывности р в х. Второе условие, имеющее смысл только при р(x) ≠ 0, обеспечивает сходимость (по вероятности) отношения частот к вероятности Р.
Совершенно ясно, что третье условие необходимо, если рn(x), заданная соотношением (2.10.5), вообще должна сойтись. Это условие говорит также о том, что, хотя в конечном счете в небольшую область Rn попадает огромное количество выборок, оно составит лишь незначительно малую часть всего количества выборок.
Существует два общих способа получения последовательностей областей, удовлетворяющих указанным выше условиям. Первый способ заключается в сжатии начальной области за счет определения объема Vn, как некоторой функции от n, такой, чтобы 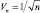 . Далее следует показать, что случайные величины kn и kn/n ведут себя правильно или, что рn(x) сходится к р(x). В этом заключается метод парзеновского окна, рассматриваемый в следующем разделе. Во втором методе kn определяется как некоторая функция от n:
. Далее следует показать, что случайные величины kn и kn/n ведут себя правильно или, что рn(x) сходится к р(x). В этом заключается метод парзеновского окна, рассматриваемый в следующем разделе. Во втором методе kn определяется как некоторая функция от n: 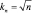 . Здесь объем Vn увеличивается до тех пор, пока не охватит kn «соседей» x. Это метод оценки по kn ближайшим соседям. Оба эти метода действительно обеспечивают сходимость, хотя трудно сказать что-либо определенное об их поведении при конечном числе выборок.
. Здесь объем Vn увеличивается до тех пор, пока не охватит kn «соседей» x. Это метод оценки по kn ближайшим соседям. Оба эти метода действительно обеспечивают сходимость, хотя трудно сказать что-либо определенное об их поведении при конечном числе выборок.
Парзеновские окна
Зададим область Rn в виде d-мерного гиперкуба, длина ребра которого равна hn и, следовательно, объем равен
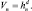
Определим функцию окна:
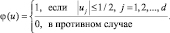
Таким образом, φ(u) определяет единичный куб с центром в начале координат. Отсюда следует, что 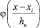 равняется единице, если xi находится в гиперкубе объема Vn с центром в x, или нулю в любом другом случае. Следовательно, количество выборок в этом гиперкубе задается выражением:
равняется единице, если xi находится в гиперкубе объема Vn с центром в x, или нулю в любом другом случае. Следовательно, количество выборок в этом гиперкубе задается выражением:
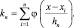
Подставляя полученное выражение в (1.10.5), получаем оценку плотности вероятности:
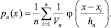 (2.10.6)
(2.10.6)
Полученная оценка должна быть неотрицательна с площадью, равной 1. Для этого необходимо:
φ(u) ≥ 0; 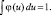
Достоинство рассмотренного метода заключается в том, что при достаточно большом числе выборок оценка плотности вероятности сходится к неизвестной плотности. В то же время требуемое число выборок может оказаться чрезвычайно большим. Это число может быть оказаться слишком велико для реальной ситуации, причем практически отсутствуют способы уменьшения требуемого объема данных. Более того, потребность в числе выборок растет экспоненциально с увеличением размерности пространства признаков.
