Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.10.6. Множественный дискриминантный анализ
Для задачи с M классами естественное обобщение линейного дискриминанта Фишера включает (M – 1) разделяющих функций.
Таким образом, проекция будет из d-мерного пространства на (M – 1)-мерное пространство, причем принимается, что d ≥ M. Обобщение для матрицы разброса внутри класса очевидное:
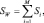
где, как и прежде,
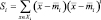
и
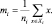
Соответствующее обобщение для SB не так очевидно. Предположим, что определяем полный вектор средних значений m и полную матрицу разброса ST посредством
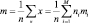
и
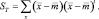
Отсюда следует, что
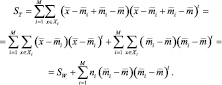
Естественно определять этот второй член как матрицу разброса между классами, так что полный разброс есть сумма разброса внутри класса и разброса между классами:
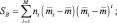
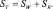
Проекция из d-мерного пространства в (М – 1)-мерное пространство осуществляется с помощью М – 1 разделяющих функций
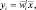i = 1, ..., M – 1.
Если считать yi составляющими вектора 
, а векторы весовых функций 
столбцами матрицы W размера d′(M – 1), то проекцию можно записать в виде одного матричного уравнения
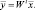
Выборки y1, …, yn проецируются на соответствующее множество выборок x1, …, xn, которые можно описать с помощью их векторов средних значений и матриц разброса. Так, если мы определяем
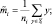
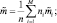
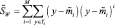
и
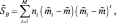
то можно непосредственно получить
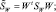
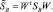
Эти уравнения показывают, как матрицы разброса внутри класса и между классами отображаются посредством проекции в пространство меньшей размерности. Находим матрицу отображения W, которая в некотором смысле максимизирует отношение разброса между классами к разбросу внутри класса. Простым скалярным показателем разброса является определитель матрицы разброса. Определитель есть произведение собственных значений, а, следовательно, и произведение дисперсий в основных направлениях, измеряющее объем гиперэллипсоида разброса. Пользуясь этим показателем, получим функцию критерия
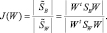
Задача нахождения прямоугольной матрицы W, которая максимизирует J, достаточно сложна. К счастью, оказывается, что ее решение имеет относительно простой вид. Столбцы оптимальной матрицы W являются обобщенными собственными векторами, соответствующими наибольшим собственным значениям в
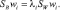
Следует сделать несколько замечаний относительно данного решения. Во-первых, если Sw – невырожденная матрица, то данную задачу можно свести к обычной задаче определения собственного значения. Однако в действительности это нежелательно, т.к. при этом потребуется ненужное вычисление матрицы, обратной Sw. Вместо этого можно найти собственные значения как корни характеристического полинома
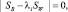
а затем решить
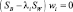
непосредственно для собственных векторов wi. Поскольку SB является суммой M матриц ранга единица или менее и поскольку только M – 1 из них независимые матрицы, постольку SB имеет ранг (M – 1) или меньше. Так что не более M – 1 собственных значений не нули и искомые векторы весовых функций соответствуют этим ненулевым собственным значениям. Если разброс внутри класса изотропный, то собственные векторы будут просто собственными векторами матрицы SB, а собственные векторы с ненулевыми собственными значениями стягивают пространство, натянутое на векторы mi – m. В этом частном случае столбцы матрицы W можно найти, просто применяя процедуру ортонормирования Грама–Шмидта к M – 1 векторам mi. Наконец, заметим, что, вообще говоря, решение для W не является однозначным. Допустимые преобразования включают вращение и масштабирование осей различными путями. Это все линейные преобразования из (M – 1)-мерного пространства в (M – 1)-мерное пространство, и они не меняют значительно положения вещей. В частности, они оставляют функцию критерия J(W) инвариантной.
Как и в случае с двумя классами, множественный дискриминантный анализ в первую очередь позволяет сократить размерность задачи. Параметрические или непараметрические методы, которые могут не сработать в первоначальном (многомерном) пространстве, могут хорошо действовать в пространстве меньшей размерности.
Например, можно будет оценить отдельные ковариационные матрицы для каждого класса и использовать допущение об общем многомерном нормальном распределении после преобразования, что было невозможно сделать с первоначальными данными. Вообще преобразование влечет за собой некоторое ненужное перемешивание данных и повышает теоретически достижимый уровень ошибки, а проблема классификации данных все еще остается.