Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.1.1. Синтез оптимального измерителя общегруппового параметра групповой цели
В настоящем разделе рассмотрено решение задачи оптимального измерения координаты общегруппового центра распределенной цели. Вся доступная информация о пространственном положении цели содержится в апостериорной плотности вероятности
,
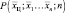где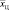 
– координата общегруппового центра цели, n – число отсчетов полученного РЛИ, 
– пространственные координаты отдельных элементов группы относительно общегруппового центра.
Определяющее значение для решения задачи синтеза устройства оценки общегруппового центра имеет апостериорная плотность вероятности
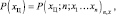(5.1.1)
поскольку принятие решения заключается в определении какого-либо параметра названной плотности (математического ожидания, моды и т.д.), выбор которого зависит от принятого критерия (минимум среднеквадратической ошибки, максимум апостериорной вероятности и т.п.).
В выражении (5.1.1) усреднение производится по всем возможным значениям как числа элементов цели, так и комбинациям их пространственных координат.
При заданной априорной вероятности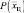 
и коэффициенте правдоподобия 
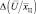выражение апостериорной плотности вероятностей определяется по формуле Байеса
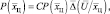(5.1.2)
где 
– вектор комплексных амплитуд наблюдаемых данных.
Коэффициент правдоподобия в формуле (5.1.2) определяется статистическим усреднением частного коэффициента правдоподобия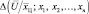 
, записанного в предположении, что координаты элементов цели известны и фиксированы, по всем возможным значениям вектора 
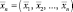координат отдельных точек ПРЦ
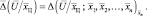(5.1.3)
Усреднение в (4.1.3) производится по плотностям вероятности
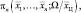(5.1.4)
содержание которых заключается в следующем. Вероятность ΔPn нахождения в области пространства Ω, занятой целью, ровно n целей, координаты которых попали в интервалы
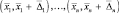
при условии, что координата центра цели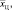 
с точностью до величин второго порядка малости относительно 
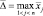, выражаются в виде
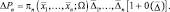(5.1.5)
При сделанных предположениях операция усреднения (5.1.3) может быть конкретизирована следующим образом:
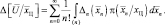(5.1.6)
Индекс (n) под интегралом указывает на его кратность, причем область интегрирования равна Ω – интервалу возможных координат элементов цели.
Если сигналы разрешены по каждой из своих координат, то справедливо выражение:
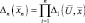(5.1.7)
и, следовательно, для (4.1.6) можно записать:
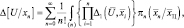(5.1.8)
где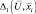 
– коэффициент правдоподобия для цели, состоящей из одного элементарного отражателя с пространственной координатой 
.
В соответствии с методикой [1] более удобной по сравнению с (5.1.4) вероятностной характеристикой для задания расположения элементов ПРЦ может служить производящий функционал
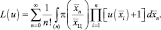(5.1.9)
Производящий функционал (5.1.9) позволяет выразить апостериорные характеристики многоэлементной цели в более компактной форме для ряда важных случаев. Это, в первую очередь относится к тем статистическим ситуациям, когда: цели разрешены по всем координатам, а априорные координаты отдельных элементов групповой цели представляют собой поток Пуассона или Бернулли.
Во избежание громоздких выкладок в дальнейшем подробно рассмотрим задачу в одномерном варианте, а именно, определим алгоритм оценки одной координаты общегруппового параметра цели (центра ПРЦ) и оценим его эффективность для ряда важных практических приложений. Такой подход по существу не снижает общности основных выводов и рекомендаций существенно упрощая решение задачи синтеза и анализа.
Сравнивая выражения (5.1.8) и (5.1.9), нетрудно установить следующее соотношение:
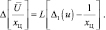(5.1.10)
Априорная информация о координатах отдельных элементов групповой цели задается ниже в двух вариантах:
а) координаты отдельных целей представляют собой поток Пуассона;
б) координаты отдельных целей аппроксимируются потоком Бернулли.
Для потока Пуассона производящий функционал получен в [2]:
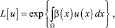(5.1.11)
где β(x) – интенсивность пуассоновского потока, заданная как функция от координаты цели.
Сравнение выражений (5.1.11) и (5.1.10) позволяет непосредственно получить выражение для усредненного коэффициента правдоподобия при моделировании отсчетов РЛИ ПРЦ пуассоновским потоком
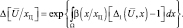(5.1.12)
Принятое для интенсивности потока обозначение β(x/xЦ) подчеркивает зависимость интенсивности от измеряемого параметра – координаты центра сложной цели хЦ.
Для другого частного случая, когда поток координат элементов поверхности РЛИ ПРЦ аппроксимирован потоком Бернулли, выражение производящего функционала имеет вид:
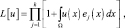(5.1.13)
где k – максимальное число отдельных элементов групповой цели (число элементов разрешения, приходящихся на цель максимально возможных размеров); ej(x) – парциальная плотность вероятности наличия отражающего элемента на j-й позиции (с номером j), не обязательно нормированная к единице, то есть
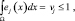(5.1.14)
что допускает отсутствие отражающего элемента цели в j-м элементе разрешения с вероятностью
μj = 1 – νj . (5.1.15)
Сравнение выражений (5.1.10) и (5.1.13) позволяет получить коэффициент правдоподобия
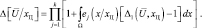(5.1.16)
С учетом (5.1.14) и (5.1.15) последнее выражение может быть записано в следующем виде
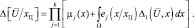(5.1.17)
В тех случаях, когда решение принимается по критерию максимума апостериорной плотности вероятности, оценка координаты центра цели находится из выражения
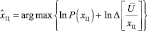(5.1.18)
и определяется формулами:
для пуассоновского потока
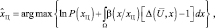(5.1.19)
для потока Бернулли
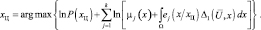(5.1.20)
Соответствующие схемы изображены на рис. 5.1 и 5.2.
Как в том, так и другом случае основная функциональная операция состоит в обобщении данных оптимальных приемников первичной обработки (интегрировании по ожидаемой протяженности цели с весами, определяемыми априорным изменением интенсивности потока с соответствующим «загрублением» разрешающей способности).
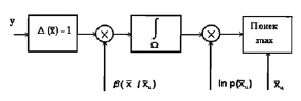
Рис. 5.1. Блок-схема измерителя координаты центра (поток Пуассона)
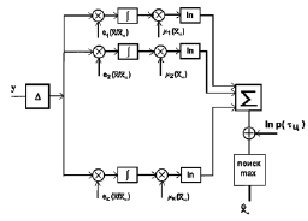
Рис. 5.2. Блок-схема измерителя координаты центра (поток Бернулли)
Таким образом, для построения классического байесовского измерителя необходимо априорное знание интенсивности потока β(х/хЦ) или парциальных плотностей е(х), которые должны рассчитываться, исходя из принятых моделей отдельных ПРЦ и/или тактики построения.