Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.4. Анализ алгоритмов оценки координат граничных точек между областями РЛИ с отличающимся контрастом
Эффективность алгоритмов оценки координат граничных точек производилась методом статистического моделирования. Названным методом генерировалось выборочное РЛИ в одном канале дальности, содержащее 100 случайных отсчетов, первая половина которых имела плотность вероятности с одним параметром (σ1), а вторая половина – с другим (σ2). Величина ошибки Δn рассчитывалась как сумма смещения и среднеквадратичного отклонения оценки координаты точки изменения параметра (вычисленная в количестве отсчетов РЛИ, что эквивалентно количеству элементов разрешения). На рис. 5.6 показана зависимость ошибки от величины отношения ЭПР цели и фона в одном элементе разрешения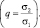 
Зависимости получены для следующих распределений отсчетов:
1 – гамма-распределение;
2 – экспоненциальное распределение (с известными априори параметрами);
3 – экспоненциальное распределение с неизвестными параметрами.
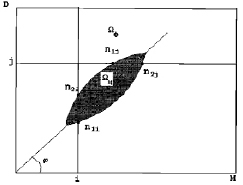
а
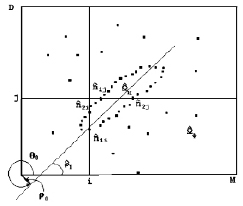
б
Рис. 5.6. К выводу алгоритмов оценки области РЛИ, занимаемой ПРЦ, и ракурса цели
Из приведенного рисунка следует, что качество алгоритмов оценки граничных точек существенно зависит от вида распределения отсчетов РЛИ, причем названная зависимость тем сильнее, чем меньше радиолокационный контраст между поверхностью цели и МП. При этом экспоненциальное распределение представляет собой наименее благоприятную ситуацию для качественного воспроизведения цели. Однако, при контрасте более 8 дБ качество оценки координат граничных точек практически не зависит от вида распределения отсчетов и от наличия априорной информации об их параметрах. Адаптивный алгоритм в условиях произведенного моделирования практически не уступает оптимальному.
Зависимость ошибки Δn от общего количества отсчетов показана на рис. 5.7. Очевидно, что уменьшение размеров фрагмента РЛИ, по которому принимается решение о наличии и координате скачка ЭПР, приводит к возрастанию ошибки. Кроме того, ошибка растет тем больше, чем дальше расположена точка скачка ЭПР от середины фрагмента, поскольку уменьшается число отсчетов и, следовательно, качество оценки одного из параметров распределения (рис. 5.7). Улучшение оценки второго параметра не компенсирует потерь, возникающих при оценке первого (При расположении скачка на краях фрагмента ошибка существенно выше).
На рис. 5.8 показана оценка контура цели на РЛИ размером 100×100. Распределение отсчетов – экспоненциальное, алгоритм адаптивный.
Зависимость ошибки Δn от общего количества отсчетов показана на рис. 4.6. Очевидно, что уменьшение размеров фрагмента РЛИ, по которому принимается решение о наличии и координате скачка ЭПР, приводит к возрастанию ошибки. Кроме того, ошибка растет тем больше, чем дальше расположена точка скачка ЭПР от середины фрагмента, поскольку уменьшается число отсчетов и, следовательно, качество оценки одного из параметров распределения (рис. 5.7). Улучшение оценки второго параметра не компенсирует потерь, возникающих при оценке первого (При расположении скачка на краях фрагмента ошибка существенно выше).
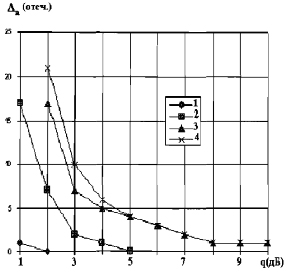
Рис. 5.7. Средняя ошибка оценки координат граничных точек контура цели в зависимости от среднего радиолокационного контраста при нормальном распределении отсчетов РЛИ (1), гамма-распределении (2), экспоненциальном с известными (3) и неизвестными (4) параметрами
Для оценки длины цели в одном канале РЛИ определялись координаты двух точек изменения параметров РЛИ (начальной и конечной). Зависимость ошибки оценки длины ΔL от величины отношения параметров q показана на рис. 5.7. Ошибка ΔL вычислялась как сумма смещения и среднеквадратического отклонения длины цели в одном канале (усреднение производилось по 50 испытаниям). Из рисунка следует, что эффективность оптимального и адаптивного алгоритмов практически одинакова и составляет величину порядка одного отсчета при контрасте порядка 6–7 дБ.
а
б
в
Рис. 5.8. Пример оценки контура цели (а) адаптивным алгоритмом при двух значениях среднего радиолокационного контраста