Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.7.2. Анализ алгоритма
Относительный выигрыш оптимальной обработки по сравнению с традиционной в РСА не позволяет оценить абсолютные значения характеристик обнаружения при многоэлементных источниках сигнала и помех. С другой стороны, точный расчёт названных характеристик связан со значительными вычислительными трудностями, возникающими при определении и интегрировании распределённой статистики (5.7.10). В связи с этим для оценки эффективности рассматриваемого алгоритма использована методика, основанная на границе Чернова [3], в соответствии с которой вероятности правильного обнаружения и ложной тревоги могут быть рассчитаны по формулам:
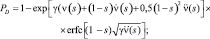(5.7.16)
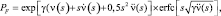(5.7.17)
где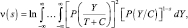 
(5.7.18)
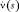и 
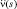– первая и вторая производные от (5.7.18); s = 0…1 – фиктивный параметр; γ – число независимых испытаний (практически для РСА – это количество используемых частот при многочастотном зондировании или число некогерентно суммируемых синтезированных изображений при частично когерентном режиме работы РСА); P(Y/(T + C)), P(Y/C) – плотности вероятностей наблюдаемого вектора при наличии и отсутствии полезного сигнала.
Для случая, рассматриваемого в работе, выражение (5.7.18) имеет вид
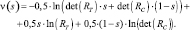(5.7.19)
По формулам (5.7.16) и (5.7.17) с учётом выражения (5.7.19) и его производных рассчитаны рабочие характеристики и характеристики обнаружения.
Рабочие характеристики, приведенные на рис. 5.17–5.19 построены для случая, когда имеется лишь одна цель и одна помеха, 
, а число периодов наблюдения M = 1300. На графиках также приведены рабочие характеристики для случаев отсутствия помехи и обработки, не использующей представленный в статье алгоритм.
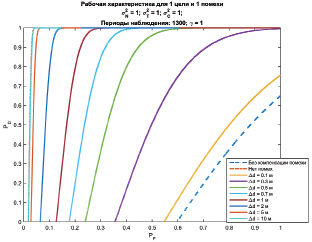
Рис. 5.17. Рабочие характеристики для переменного значения Δd
На рис. 5.17 приведены кривые для различных значений расстояния между целью и помехой Δd при γ = 1. По графику видно, что обработка с применением описанного в статье алгоритма позволяет улучшить характеристики обнаружения даже при γ = 1. С увеличением расстояния между целью и помехой, начиная с 10 м, рабочая характеристика приближается к случаю, когда помеха отсутствует полностью.
На рис. 5.18 и 5.19 приведены кривые для различных значений числа испытаний γ при Δd = 20 м для разных интервалов по оси абсцисс. С увеличением числа независимо проведенных испытаний γ характеристики обнаружения имеют существенный выигрыш в сравнении с обработкой без компенсации помех.
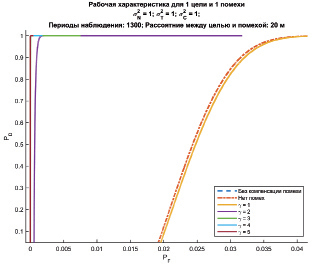
Рис. 5.18. Рабочие характеристики для переменного значения γ
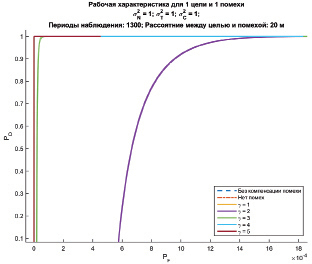
Рис. 5.19. Рабочие характеристики для переменного значения γ
Характеристики обнаружения многоэлементной цели (n = 5) на фоне многоэлементной помехи (N = 5) при 
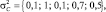M = 100, γ = 2 для помеховых ситуаций с различными взаимными угловыми расположениями цели и помех (рис. 5.20) приведены на рис. 5.21. Из представленных кривых следует, что при большем пространственном разделении цели и помех алгоритм позволяет существенно повысит вероятность обнаружения цели.