Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Современное состояние и оценка эффективности использования инвестиционных ресурсов в аграрном секторе.

Топсахалова Ф. М.-Г., Лепшокова Р. Р., Койчуева Д. А.,

4.3.6. Анализ альтернативы “риск-доходность”

Хотя доход от инвестирования не обязательно гарантирован, именно ожидаемый доход побуждает людей вкладывать средства в данный объект. Отсутствие указанной гарантии означает наличие риска, под которым обычно понимают вероятность отклонения величины фактического инвестиционного дохода от величины ожидаемого. Чем изменчивее и шире шкала колебаний доходов, тем выше риск и наоборот.

В фундаментальном учебнике проблемы измерения инвестиционного дохода и риска предлагается решать на базе альтернативы (риск-доходность). Альтернатива "риск-доходность" - это отношение между риском и доходностью, показывающее, обеспечивают ли более рискованные инвестиции более высокую доходность и наоборот. Более рискованные инвестиции должны обеспечивать более высокую доходность. Суть проблемы состоит в том, чтобы в альтернативе "риск-доходность" определить наиболее целесообразный вариант, т.е. в нашем случае осуществить наилучший выбор объекта х из множеств Х.

Построение математической модели альтернативы "риск-доходность" базируется на следующих предложениях.

Величина ожидаемой доходности является случайной величиной для принимающей некоторые численные значения, для который, однако, распределение вероятностей неизвестно. Мы предполагаем, что присущий данному объекту х характер поведения временного ряда значений доходности за прошлые годы сохраняет свои особенности, на следующие годы рассматриваемого планового периода. Из этого предложения следует, что с некоторой погрешностью можно представить значение ожидаемой доходности Di = Di(x) и значение вероятностей

Pi = Pi (x), i = 1,2,...4, ,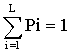

с которыми указанные значения доходности могут достигаться.

В принятых обозначениях ожидаемая доходность вычисляется в виде математического ожидания

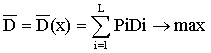                                          (13)

представляющего собой минимизирующий критерий доходности. Далее вычисляя СКО

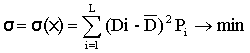                                  (14)

получаем коэффициент вариации

V = Vx = 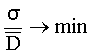                                         (15)

Представленные выражения (14) и (15) СКО и коэффициент вариации по аналогии с (11) и (12) может рассматривать в качестве минимизируемых критериев степени риска.

Как мы уже отмечали в настоящее время общепризнанным современным измерителем риска является фактор «бета», который, к сожалению, невозможны вычислить для существенной реальных условий отечественного АПК. Для того, чтобы выполнить указанную невозможность использования фактора «бето», предлагается ввести в рассмотрение такие показатели как коэффициент ассиметрии

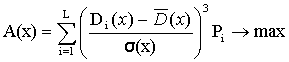                                   (16)

и коэффициент эксцесса

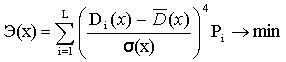                                              (17)

Содержательный смысл этих коэффициентов состоит в следующем. Возрастание величины А(х) означает проявление благоприятной тенденции, когда увеличивается вероятность появления значений доходности, превосходящих величину математического ожидания (13). Наоборот, убывание величины А(х) означает, что проявление неблагоприятной тенденции, когда увеличивается вероятность появления значений доходности строго меньших величины математического ожидания.

Экономический смысл коэффициент асимметрии применительно к рассматриваемой проблеме рисков, заключается в следующем. В случае возрастания коэффициента (16) возрастает вероятность появления самых высоких доходов и убывает вероятность самых низких доходов. Иногда образно эту тенденцию называют термином «правый хвост». Соответственно, случай уменьшения коэффициента (16) проявляется тенденция образования «левого хвоста», т.е. более вероятным будут считаться низкие доходы.

Отсюда вытекает, что асимметрия является максимизируемым критерием характеризующим степень риска.

Охарактеризуем рисковый смысл, который отражается коэффициентом эксцесса, в процессе его изменения в сторону увеличения или уменьшения. Увеличение значения Э(х) приводит к тому, что график функции плотности вероятностей случайной величины дохода D(х) становится менее «островершинным», т.е. этот график становится приплюснутым и растянутым. Последнее свойство «растянутости» означает расширение области значений ожидаемой доходности в обе стороны, удаление от величины математического ожидания D(х). Очевидно, усиление этого свойства можно трактовать как возрастание вероятности получить малое значение доходности и уменьшение вероятности получить среднее значение доходности.

В то же время уменьшение значения коэффициента эксцесса (17) приводит к тому, что график функций плотности вероятности случайной величины D(х) вытягивается вверх, сужая при этом разброс значений доходности в окрестности значений математического ожидания. Очевидно, что усиление этого свойства можно трактовать как возрастание вероятности получить значение доходности, близкое к среднему и уменьшение вероятности получить малое значение доходности.

Из всего вышесказанного вытекает, что критерий представленной коэффициентом эксцесса (17) является минимизируемым.