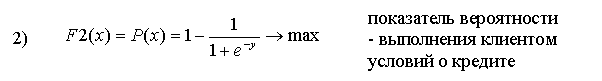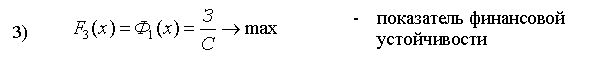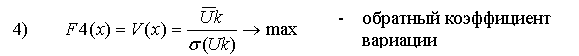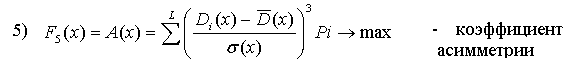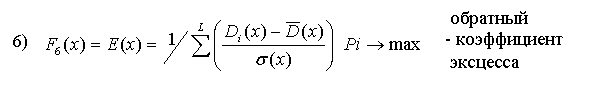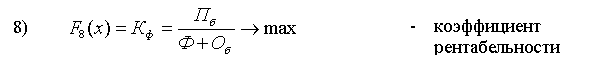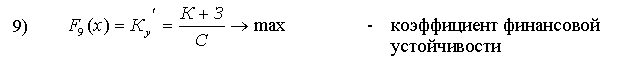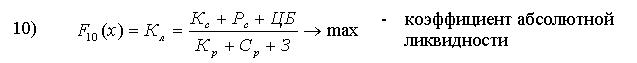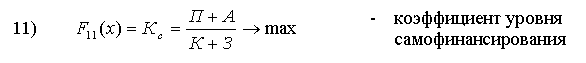Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Современное состояние и оценка эффективности использования инвестиционных ресурсов в аграрном секторе.

Топсахалова Ф. М.-Г., Лепшокова Р. Р., Койчуева Д. А.,

4.4.6. Построение векторно-целевой функции (1) и конкретизация состава ее критериев

Основная цель предлагаемой экономико-математической модели состоит в том, чтобы предоставить инвестору возможность всесторонней оценки инвестиционной привлекательности объектов х Х с последующим ранжированием их по убыванию степени предпочтительности этих объектов. Основным инструментом для достижения этой цели является ВЦФ1.

Возникает вопрос: можно ли построить эту ВЦФ путем механического объединения всех перечисленных выше критериев в один вектор, представляющий правую часть выражения (1). Ответ на этот вопрос вообще отрицательный, такое механическое объединение допустимо лишь в том случае, если множество всех объектов Х содержит вариант х⁰, вариант, относительно которого можно утверждать, что он не хуже любого другого варианта х Х по каждому из критериев (2) - (3).

Однако, в реальных ситуациях существование х⁰ мало вероятно. В таком случае возникает проблема определения наиболее предпочтительного решения, среди элементов Паретовского множества х Х.

Для практического решения сформулированной проблемы выбора, используем так называемые прямые методы [1]. Удобная для практического использования реализация этих методов предложена в [2] в виде так называемого обобщенного решающего правила (ОРП).

Использование ОРП требует, чтобы ВЦФ1 удовлетворяла следующим условиям:

1. Критерии F_v(x), v = составляющая ВЦФ должны быть однородными экстремума: либо все критерии данной ВЦФ являются минимизируемыми, либо все они являются максимизируемыми.

2. Условия соизмеримости: все критерии данной ВЦФ имеют одну и ту же единицу измерения.

В отношении пункта 1 выскажем следующее замечание. Если ВЦФ состоит из максимизируемых и минимизируемых критериев, то чаще всего п.1 является более предпочтительным, поскольку они позволяют удобным образом осуществить нормирование их значений. Согласно формуле

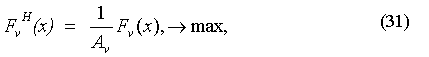
где А_v =  F_v (х) - представляет собой значения максимизируемых критериев F_v(х) → max, которое он достигает на своем оптимальном решении. Нормированная величина (31) выражает значение F_v(х) в долях от величины оптимума А_v . Таким образом, в случае, если все критерии ВЦФ (1) являются максимизируемыми, т.е. F_v(х) → max, v= 1,2,...,N, то ВЦФ (1), составленное из нормированных максимизируемых критериев будет полностью удовлетворять вышеуказанным условиям 1 и 2.

Как мы уже отмечали, некоторые из вышерассмотренных критериев не имеет смысла включать в состав ВЦФ (1) в силу ряда соображений: малоинформативность или несущественность с точки зрения инвестиционной привлекательности, большая погрешность в численных значениях соответствующих исходных данных и др. Представленное в п.5.3. и 5.4. показатели инвестиционной привлекательности проанализированы с учетом этих требований в результате этого анализа сформирована группа существенных показателей предлагаемых для того, чтобы на базе каждого из них полностью определить соответствующих критерий для включения ее в состав ВЦФ (1). Эта группа состоит из следующих 12 показателей, представленных соответственно формулами (4), (7), (8), (12), (12а), (15)-(17), (26)-(30):

1) Z(x) = 1,2z₁(x) + 1,4z₂(x) + 3,3z₃(x) + 0,6z₄(x) + 1,0z₅(x) → max - показатель  делового риска

 

 

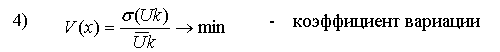
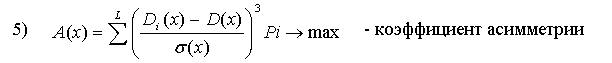
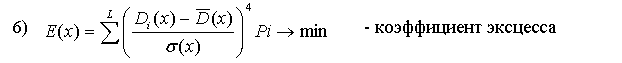
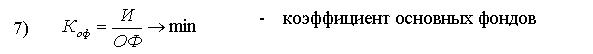
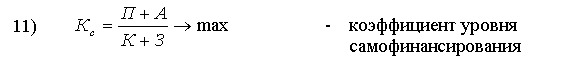
В этой группе показатели 2), 4), 6), 7) являются минимизируемыми.

Наша цель - корректно представить эти показатели в виде максимизируемых. Существую два основных подхода для достижения этой цели. Первый состоит в том, чтобы для данного исходного показателя вычислять его обратное значение, т.е. первоначальное минимизируемое значение возводить в степень (-1). Второй подход состоит в том, чтобы определить некоторую подходящую С F_v (х) и рассматриваемый минимизируемый критерий F_v (х) заменить на максимизируемый критерий F_v^' (х) = С_v - F_v (х). Какой из этих подходов применять, зависит от конкретного формального определения и финансово-экономического содержания F_v (х). Например, если в представленном выше списке показателей рассмотреть второй, являющийся вероятностью Р(х) → min, то совершенно очевидно, что при замене на максимизируемый показатель нужно применять второй подход, выбирая в качестве С_v константу С₂ = 1. В результате получим максимизируемый показатель Р^'(х) = 1 - Р(х).

Для оставшихся трех минимизируемых показателей 4) V_x, 6) E(x) и 7) К_оф используем первый подход, с целью замены их на максимизируемые показатели. В результате указанных преобразований получаем N =12 максимизируемых критериев F_v(x) → max, v = 1,2,...11 составляющих ВЦФ (1).

В процессе указанных преобразований семь минимизируемых показателей первоначального списка изменили свой содержательный смысл. В окончательном представлении этот список имеет следующий вид:

1)      F1(x) = Z(x) = 1,2z₁(x) + 1,4z₂(x) + 3,3z₃(x) + 0,6z₄(x) + 1,0z₅(x) → max -  показатель делового риска