Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные методы оптимизации

Шукаев Д. Н.,

1.2. Метод безусловной оптимизации

Задачу безусловной оптимизации получим из (1.2) приняв m = 0. В начале также предположим, что число переменных n = 1, что соответствует одномерной задаче максимизации целевой функции от скалярного аргумента. Тогда имеем

f(x) > max. (1.4)

Если x* – точка локального максимума f(x), то очевидно

f(x*) ≥ f(x + Δx), (1.5)

где Δx – малое приращение аргумента. Учитывая, что f(x) непрерывная функция разложим ее в ряд Тейлора

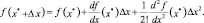
Подставив в неравенство (1.5) получим основное неравенство

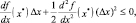(1.6)

которое должно выполняться для любого произвольно малого приращения Δx.

Если Δx больше нуля, то разделив обе части на Δx > 0 и переходя к пределу Δx → 0 получим

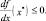
Аналогично при Δx < 0 приходим к

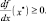
Тогда в качестве необходимого условия получаем, что первая производная в точке локального максимума равна нулю

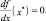(1.7)

Поэтому из выражения (1.6) учитывая, что (Δx)² всегда положительное число, приходим к необходимому условию, что в точке локального максимума вторая производная отрицательна или равна нулю

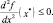(1.8)

Очевидно, достаточным условием строгого локального максимума будет

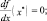
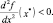(1.9)

Геометрическая интерпретация изложенных выкладок показана на рис. 1.1. [15]

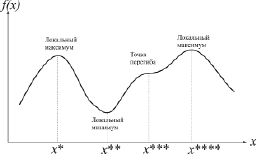
Рис. 1.1. Точки экстремума

Как видно из рисунка, угловой коэффициент касательной к кривой f(x) в точке х = x* равен нулю, причем величина углового коэффициента убывает. Следовательно, по условию (1.9) точка х = x* соответствует строгому максимуму. А в точках х = x** и х = x*** условие второго порядка нарушено, т.е. угловой коэффициент касательной к кривой f(x) в первом случае возрастает, а во втором остается постоянным.

Общую задачу безусловной оптимизации при n > 1

f(x) = f(x1, x2, …, x_n) → max (1.10)

можно исследовать по аналогии c одномерным случаем, рассмотренным выше.

Допустим, что локальный максимум существует в точке x*, следовательно

f(x*) ≥ f(x* + hΔx), (1.11)

где h – малое положительное число, а Δx определяет некоторое направление в Еⁿ.

Рассматривая функцию в правой части неравенства (1.11) как функцию от h разложим ее по формуле Тейлора в окрестности точки h = 0

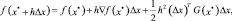(1.12)

где G(x*) – матрица Гесса размерности n ×n с элементами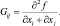

Сопоставляя выражения (1.12) и (1.11) получим основное неравенство для многомерной задачи безусловной оптимизации, которое должно выполняться для всех направлений Δx и для всех малых положительных чисел h.

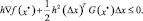(1.13)

Чтобы вывести из основного неравенства необходимое условие первого порядка, разделим обе части (1.13) на h и перейдем к пределу при h стремящемся к нулю. В итоге получаем, что в точке локального максимума (стационарная точка) градиент функции равен нулевому вектору

∇f(x*) = 0. (1.14)

Из основного неравенства также следует, что в точке локального максимума матрица Гессе отрицательно определена или отрицательно полу определена

G(x*) ≤ 0

для всех Δx. Очевидно, что для достижения строгого локального максимума выполняется условие

∇f(x*) = 0, G(x*) < 0. (1.15)

Для конкретности покажем эти условия на функции двух переменных

f(x1, x2) > max.

Напишем условия первого порядка существования локального максимума

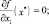
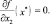(1.16)

Необходимые условия второго порядка – это отрицательная определенность или отрицательная полуопределенность матрицы Гессе, а это эквивалентно выполнению условий

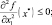(1.17)

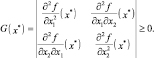(1.18)

Если в стационарной точке

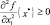и G(x*) ≥ 0, (1.19)

и если выполнено условие (1.18), то x* будет точкой локального минимума, если (1.18) не выполнено, то x* будет седловой точкой.

Пример 1.1 [19]

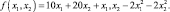
Напишем условия первого порядка существования локального экстремума

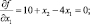
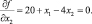
Решая эту систему уравнений получим стационарную точку

x* = (4, 6).

Для установления типа экстремума воспользуемся условиями второго порядка (1.17) и (1.18)

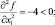
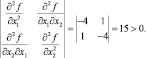
Следовательно, функция f(x) в точке (4, 6) достигает максимума.