Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.3.1. Применение аппарата дифференциального исчисления
Классический метод условной оптимизации применяется в случаях, когда целевая функция задачи оптимизации по меньшей мере дважды непрерывно дифференцируема, а ограничения не слишком сложны. Здесь возможны два подхода. Первый, прямое использование аппарата дифференциального исчисления для нахождения стационарных точек целевой функции, как это было рассмотрено выше и исследование этих точек на соответствие ограничениям задачи, а второй – преобразование целевой функции задачи так, чтобы она снова стала задачей безусловной оптимизации. Здесь наибольшее распространение получил метод множителей Лагранжа.
1.3.1. Применение аппарата дифференциального исчисления
Математическая постановка классической задачи условной оптимизации в скалярной форме имеет вид
f(x1, …, xn) > extr;
g1(x1, …, xn) = 0;
……………………;
gm(x1, …, xn) = 0.
Учитывая, что применение аппарата дифференциального исчисления для безусловной оптимизации нами подробно рассмотрено в разделе 1.2, представим его в виде укрупненного алгоритма, состоящего из следующих шагов:
Шаг 1. По необходимым условиям (1.14) существования экстремумов первого порядка находим все стационарные точки целевой функции задачи.
Шаг 2. При задании конкретного типа экстремума, например, максимума с помощью условий второго порядка (1.15) определяем, какие из стационарных точек являются кандидатами на максимум.
Шаг 3. Находим максимальные значения целевой функции, достигаемых на каждой границе допустимого множества.
Шаг 4. Сравнение значений в стационарных точках, являющимися кандидатами на максимум с максимальными значениями целевой функции, достигаемых на каждой границе допустимого множества.
Трудности, связанные с этим методом, состоят в том, что может оказаться несколько стационарных точек и много участков границ, которые нужно проверить; нахождение же экстремальных точек и максимума на каждой границе может потребовать решения систем нелинейных уравнений со всеми вытекающими отсюда неудобствами. Из-за этих трудностей классические методы приходится приспосабливать к каждой задаче индивидуально. Поэтому невозможно, используя дифференциальное исчисление, построить универсальный метод для решения широкого класса общих задач оптимизации. Однако есть и определенное достоинство этого подхода, оно заключается в том, что можно решать условную задачу оптимизации с неотрицательными переменными и при снятии требования, чтобы ограничениями были только равенства, т.е. они могут быть и неравенствами.
Пример 1.2 [19]. Пусть необходимо найти максимум функции
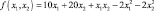
при условиях
7 – x1 ≥ 0;
8 – x2 ≥ 0;
8 – x1 – x2 ≥ 0;
x1, x2 ≥ 0.
В силу линейности ограничений область допустимых решений Х является выпуклой. Так как целевая функция непрерывна при всех вещественных значениях переменных, а допустимая область замкнута и ограничена, то по теореме Вейерштрасса существует максимум целевой функции внутри или на границе Х. В соответствии с приведенным выше обобщенным алгоритмом на первом шаге находим стационарную точку целевой функции задачи. Так как эта целевая функция была подробно рассмотрена в разделе 1.2 значение стационарной точки приведем без повторного вычисления:
x1 = 4; x2 = 6; max f = 80.
Результаты вычислений на шаге 2 также известны из раздела 1.2
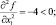G(x1, x2) = 15 > 0.
Таким образом, целевая функция всюду вогнута. Проверим является ли найденная стационарная точка кандидатом на максимум. Подставив ее значение в ограничения задачи видим, что нарушено третье ограничение и она не является допустимой. Поэтому в соответствии с шагом 3 проверим значения целевой функции на каждой границе.
а) x1 = 0. При этом условии задача примет вид:
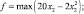
7 – 0 ≥ 0;
8 – x2 ≥ 0;
8 – x2 ≥ 0;
x2 ≥ 0.
Из двух последних ограничений следует, что x2 ∈ [0; 8]. Далее повторив для этой задачи шаги 1 и 2 получим условия первого и второго порядков
20 – 4x2 = 0, G = –4 < 0.
Следовательно
x2 = 5; max f = 50.
б) x2 = 0. При этом условии задача примет вид:
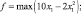
7 – x1 ≥ 0;
8 – 0 ≥ 0;
8 – x1 ≥ 0;
x1 ≥ 0.
Здесь существенным является только первое ограничение, откуда определяется верхняя граница значения x1 ∈ [0, 7], а остальные ограничения излишни. Применение условий первого и второго порядков определения стационарной точки приводит к результату
10 – 4x1 = 0; G(x1) = –4 < 0;
x1 = 2,5; max f = 12,5.
в) x1 = 7. В этом случае задача имеет вид:
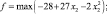
7 – 7 ≥ 0;
8 – x2 ≥ 0;
1 – x2 ≥ 0;
x2 ≥ 0.
И, соответственно, из условий первого и второго порядков имеем
27 – 4x2 = 0; G(x2) = –4 < 0,
имеем x2 = 1, max f = –3.
г) 8 – x1 – x2 = 0. Это равенство позволяет подстановкой x2 = 8 – x1 свести задачу к задаче с одной переменной
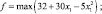
7 – x1 ≥ 0;
8 – (8 – x1) ≥ 0;
x1 ≥ 0.
Таким образом, из условий
30 – 10x1 = 0; G(x1) = –10 < 0
получим значение последней точки-претендента:
x1 = 3; x2 = 5; max f = 77.
И наконец, сравнивая значения целевой функции вдоль каждой границы убеждаемся, что максимальное ее значение равно f = 77, а оптимальным решением исходной задачи является
