Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные методы оптимизации

Шукаев Д. Н.,

1.3.2. Метод множителей Лагранжа

Этот метод применяется к классическим задачам оптимизации с ограничениями –равенствами

f(x) > extremum при g(x) = b.

Суть метода множителей Лагранжа заключается в переходе из задачи с ограничениями к задаче безусловной оптимизации введя специальную функцию Лагранжа:

L(x, λ) = f(x) + λ[g(x) – b]

или в скалярной форме

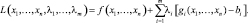
Находим частные производные функции Лагранжа

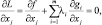i = 1, …, n;

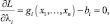i = 1, …, m.

Решением этой системы n + m уравнений являются все стационарные точки задачи. Дальше исследование найденных точек осуществляется так же, как и в случае безусловной оптимизации.

Пример 1.3. Необходимо найти экстремум функции [2]

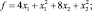
x1 + x2 = 180.

Построим функцию Лагранжа

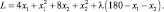
Вычислим частные производные функции Лагранжа по x1, x2, λ и приравняем их нулю

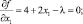
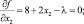
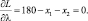
Решая эту систему уравнений находим точку – претендента на экстремум

x1 = 91; x2 = 89.

Далее вычислив частные производные второго порядка получим матрицу Гессе

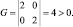
Следовательно, по условию (1.19) эта точка соответствует минимуму целевой функции задачи.