
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Контрольные вопросы и упражнения
1. При каких условиях, накладываемых на допустимое множество ограничений непрерывная целевая функция достигает глобального экстремума?
2. Какая точка называется стационарной?
3. Если в стационарной точке матрица Гессе является положительно определенной, то в этой точке имеет место максимум или минимум?
4. Если в стационарной точке матрица Гессе оказывается неопределенной, то соответствует ли эта точка экстремуму функции?
5. Для чего предназначен метод множителей Лагранжа?
6. Найдите значение максимума и минимума функции
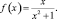
7. Покажите, что функция
f = (x1 – a)2 + (x2 – b)2 + (x3 – c)2
имеет минимум в точке (а, b, c).
8. Найдите экстремум функции
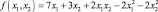
и определите вид экстремума.
9. Покажите на графике допустимое множество для классической задачи максимизации с двумя переменными и одним ограничением, где в качестве ограничений берутся следующие соотношения:
a) x1 = 10;
b) 2x1 + 4x2 = 8;
c) (x1 – 1)2 + (x2 – 6)2 = 0.
10. Найдите минимум функции
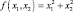
при ограничениях
x1 + x2 = 4.
11. Найдите экстремум функции
f = x1 x2 x3
при ограничениях
x1 + x2 + x3 = 5;
x1x2 + x2x3 + x1x3 = 8
и определите вид экстремума.
12. Найдите максимум функции
f = –(2x1 – 5)2 – (2x2 – 1)2
при ограничениях
x1 + 2x2 ≤ 2, x1, x2 ≥ 0
с помощью обобщенного метода множителей Лагранжа.
