
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.1. Структура задач и основные положения линейного программирования
Задачи линейного программирования, сформулированные при рассмотрении большинства прикладных задач оптимизации в экономике, производстве и в других сферах деятельности человека имеют, в общем виде, следующую математическую формулировку:
Найти максимум целевой функции
f = c1x1 + c2x2 + … + cnxn (2.1)
при соблюдении ограничений
a11x1 + a12x2 + … + a1nxn ≤ b1;
………………………………..;
am1x1 + am2x2 + … + amnxn ≤ bm;
xj ≥ 0, j = 1, …, n. (2.2)
Эти выражения в более компактной матричной форме имеют вид
f = cx; Ax ≤ b; x ≥ 0,
где х = (x1, x2, …., xn) и b = (b1, b2, …., bm) – вектор-столбцы, с = (c1, …., cn) – вектор-строка; А = (aij) – матрица размерности m×n
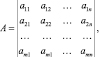
где Aj – столбцы матрицы А.
Решение х является допустимым, если оно принадлежит допустимому множеству Х
x ∈ X ={x|Ax ≤ b, x ≥ 0}.
Решение x* является оптимальным, если
cx* ≥ cx для ∀x ∈ X, (2.3)
т.е. для всех решений х, удовлетворяющих линейным ограничениям (2.2). Каждое из линейных неравенств системы ограничений определяет замкнутое полупространство и, следовательно, для допустимого множества Х справедлива следующая теорема 2.1 [19] «Допустимое множество Х задачи линейного программирования является замкнутым выпуклым множеством, имеющим не более чем конечное число крайних точек».
Следующей важной теоремой линейного программирования является теорема 2.2 «Если целевая функция принимает максимальное значение в некоторой точке допустимого множества Х, то она принимает это максимальное значение в крайней точке допустимого множества Х; если целевая функция достигает максимума более чем в одной крайней точке, то она максимальна в любой выпуклой комбинации этих точек».
