Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные методы оптимизации

Шукаев Д. Н.,

2.2. Геометрическая интерпретация задачи линейного программирования

Чтобы лучше понять суть теорем 2.1 и 2.2 рассмотрим простую задачу линейного программирования с двумя переменными.

f(x) = x1 + 3x₂ → max;

X = {x/x1 + x2 ≤ 6, x1 – x2 ≤ 2, x1 ≤ 3, x1, x2 ≥ 0}.

На основе общего подхода к оптимизации дифференцируемых функций, рассмотренных ранее, определим градиент целевой функции

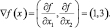
На рис. 2.1 заштрихованная площадь является областью допустимых решений Х, а линии уровней расположены перпендикулярно к вектору-градиенту. Так как вектор-градиент определяет направление наискорейшего возрастания целевой функции, то по расположению наиболее удаленной линии уровня находим оптимальную точку А с координатами:

Данный пример наглядно иллюстрирует правомерность как теоремы 2.1, так и теоремы 2.2. Одновременно, этот пример можно считать реализацией графического метода решения задачи линейного программирования с двумя переменными.

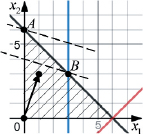
Рис. 2.1. Геометрическая интерпретация задачи