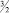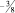Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные методы оптимизации

Шукаев Д. Н.,

2.3.3. Пошаговое описание симплекс-алгоритма

Пусть исходная задача линейного программирования представлена в канонической форме

f = c1x1 + c2x2 + … + cnxn > min;

a11x1 + a12x2 + … + a1nxn + xn+1 = b1;

a21x1 + a22x2 + … + a2nxn + xn+2 = b2;

……………………………………………;

am1x1 + am2x2 + … + amnxn + xn+m = bm;

∀xj ≥ 0 и ∀bi > 0.

Шаг 1. Построим начальную симплекс-таблицу (табл. 2.1).

Таблица 2.1

Шаг 2. Если все с_j ≥ 0, то конец – оптимальным решением является базисное решение (2.6); если некоторое значение с_j  < 0, то выбрать переменную xs, которая будет введена в базисное множество на следующей итерации вместо r-й базисной переменной, так чтобы

cs = min c_j  < 0.

Шаг 3.

а) Если все a_is ≤ 0, то конец, множество решений есть:

– x_s ≥ 0 произвольно, базисные переменные равны

x_j = b_i – a_isx_s;

– небазисные переменные x_j = 0 (j ≠ s) удовлетворяют исходной системе и обладает свойством

f = f0 + c_sx_s → –∞ при x_s → +∞.

б) Если какое-то a_is > 0, то выбираем r-ю базисную переменную, чтобы вывести ее в следующей итерации, следующим образом

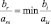при a_is > 0.

Шаг 4. Чтобы получить из предшествующей таблицы начальные данные таблицы, описывающей следующую итерацию, умножим каждый элемент выбранной строки r на число, обратное ведущему элементу ars и поместим эти произведения в r-ю строку таблицы для следующей итерации (табл. 2.2). Вводим переменную xs на место переменной xn+r в предыдущей итерации. Чтобы получить элемент, стоящий в i-й строке и j-м столбце в новой таблице, вычтем из соответствующего элемента предыдущей таблицы произведение числа, стоящего в i-й строке и s-м столбце предыдущей таблицы на число, стоящее в r-й строке и j-м столбце новой таблицы.

Таблица 2.2

где в соответствии с правилами шага 4:

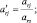
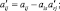
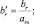
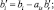
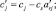
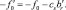
Пример 2.1.

f = –9x1 – 10x₂ – 16x₃ > min;

18x1 + 15x2 + 12x3 + x4 = 360;

6x1 + 4x2 + 8x3 + x5 = 192;

5x1 + 3x2 + 3x3 + x6 = 180;

∀xj ≥ 0.

Шаг 1. Начальная симплекс-таблица имеет вид (табл. 2.3)

Таблица 2.3

Шаг 2. cs = min {–9; –10; –16} = –16. Следовательно, s = 3.

Шаг 3.

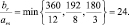
Следовательно r = 2 и ведущий элемент ars = a₂₃ = 8.

Шаг 4. Переход к следующей симплекс-таблице (табл. 2.4)

Таблица 2.4

Так как условие теоремы 2.3 не выполнено снова переходим к шагу 2.

Шаг 2. cs = –2.Следовательно s = 2.

Шаг 3.

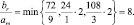
Следовательно r = 1 и ведущий элемент a_rs = a12 = 9.

Шаг 4. Переход к следующей симплекс-таблице (табл. 2.5)

Таблица 2.5

Все относительные оценки в последней симплекс-таблице не отрицательны, следовательно, в соответствии с теоремой 2.3 имеем оптимальное решение:

x1 = 0; x2 = 8; x3 = 20; x4 = 0; x5 = 0; x6 = 96; f = –400.