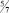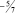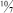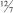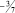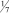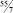Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.4.2. Связь между решениями прямой и двойственной задач
Пусть прямая задача имеет вид
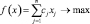 ;
;
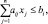 i = 1, …, m,
i = 1, …, m,
или в матричной форме
max f = cx; Ax ≤ b;
x ≥ 0.
Двойственной для нее будет задача
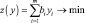 ;
;
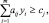 j = 1, …, n,
j = 1, …, n,
или в матричной форме
min z = yb;
yA ≥ c; y ≥ 0.
Каждая из этих задач может быть решена независимо друг от друга. Однако при определении симплекс методом оптимального решения одной из них находится и решение другой задачи.
Предположим, что с помощью симплекс метода найдено оптимальное решение прямой задачи х*, тогда по теореме 2.7 имеем
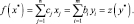 (2.9)
(2.9)
Оптимальное решение в матричной форме имеет вид
х* = А–1b,
где А–1 – обратная матрица к матрице, состоящей из элементов итоговой симплекс-таблицы. Подставляя оптимальное решение в выражение (2.9) получим
cb•А–1b = y*b,
где cb – вектор коэффициентов базисных переменных в строке целевой функции, вошедших в оптимальное решение. Тогда оптимальное решение двойственной задачи равен
y* = cb•А–1.
Проиллюстрируем сказанное на конкретном примере 2.2.
Пример 2.2.
Дана задача линейного программирования
max f = 4x1 + 5x2 + 9x3 + 11x4;
x1 + x2 + x3 + x4 ≤ 15;
7x1 + 5x2 + 3x3 + 2x4 ≤ 120;
3x1 + 5x2 + 10x3 + 15x4 ≤ 100;
∀xj ≥ 0.
Тогда двойственная задача имеет вид
min Z = 15y1 + 120y2 + 100y3;
y1 + 7y2 + 3y3 ≥ 4;
y1 + 5y2 + 5y3 ≥ 5;
y1 + 3y2 + 10y3 ≥ 9;
y1 + 2y2 + 15y3 ≥ 11;
∀yj ≥ 0.
Решая прямую задачу получим следующую итоговую симплекс-таблицу (табл. 2.6).
Таблица 2.6
|
БП |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
bi |
|
x1 |
1 |
|
|
|
|
|
||
|
x3 |
|
1 |
|
|
|
|
||
|
x6 |
|
|
|
1 |
|
|
||
|
–f |
|
|
|
|
|
Таким образом оптимальным решением исходной задачи будет
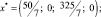
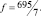
А оптимальное решение двойственной задачи определяется значениями коэффициентов f – cтроки итоговой симплекс-таблицы (табл. 2.6):
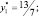

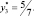
Убедимся, что ограничения двойственной задачи выполняются
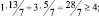
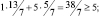
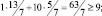
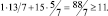
и что в соответствии с теоремой 2.7 значение целевой функции двойственной задачи совпадает с оптимальным значением целевой функции исходной задачи