Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.4.3. Экономическая интерпретация двойственной задачи
Экономическую интерпретацию покажем на задаче производственного планирования, рассмотренной в начале пункта 2.4.1. Пусть х оптимальное решение задачи
max f = cx,
Ax ≤ b;
x ≥ 0.
Выясним как будет меняться оптимальное решение x* при изменений компонент вектора b и, в частности, при каких вариациях b + Δb оптимальное решение остается неизменным? Это, так называемая, проблема устойчивости оптимального решения. Действительно, на практике объемы доступных ресурсов могут колебаться после принятия плановых решений. Поэтому предположим, что вектор ресурсов b может изменится на величину Δb и это приведет к появлению вариации оптимального решения x*(b + Δb) и целевой функции f(x*(b + Δb)). Рассмотрим отношение приращения целевой функции к приращению ресурса Δb. Если для некоторого i устремить Δbi → 0, то получим
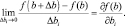
Учитывая, что в соответствии с теоремой 2.7
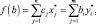
получим
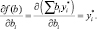
Из этого соотношения вытекает экономическая интерпретация оптимальных переменных двойственной задачи. Каждый элемент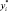 
может рассматриваться как предельная оценка вклада i-го ресурса в суммарный доход f при оптимальном решении х*, т.е. величина 
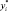равна приросту дохода, возникающему при увеличении ресурса i на единицу при условии оптимального использования ресурсов.
На основе теорем двойственности для пары задач линейного программирования могут быть сформулированы некоторые важные (с точки зрения экономической интерпретации) следствия [21]:
если для оптимального решения исходной задачи i-е ограничение выполняется как строгое неравенство:
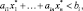
то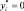 
, следовательно, bi-й ресурс в избытке и это ограничение становится несущественным и оценка (теневая цена) такого ресурса равна нулю;
если для оптимального решения двойственной задачи j-е ограничение выполняется как строгое неравенство
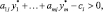
то оптимальное значение соответствующей переменной исходной задачи равно нулю. Действительно, при превышении удельных затрат над доходом от j-го продукта его производство будет нерентабельным и поэтому должно быть
.
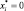