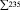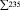Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.3. Нахождение оптимального решения транспортной задачи
Для определения оптимального решения транспортной задачи также разработаны несколько методов: потенциалов, венгерский и другие, однако наибольшее распространение получил метод потенциалов. Суть этого метода похожа по принципу на симплекс-метод. С начало определяют допустимое базисное решение (например, методом минимальной стоимости), затем его улучшают до получения оптимального решения. Этот метод основан на следующей теореме 3.4 [21] «Если для некоторого допустимого базисного решения xb = {xij} транспортной задачи существуют такие числа
α1, α2, …, αm, β1, β2, …, βn,
что
βj – αi = cij при xij > 0; (3.2)
βj – αi ≤ cij при xij = 0 (3.3)
для всех i = 1, 2, …, m и j = 1, 2, …, n, то xb = {xij} – оптимальное решение транспортной задачи».
Числа αi и βj называются соответственно потенциалами пунктов отправления и назначения.
Условия (3.2) и (3.3) имеют содержательную интерпретацию. Потенциалы αi и βj можно рассматривать как цены на перевозимую продукцию в пунктах отправления и назначения. Тогда, согласно условию (3.2), для оптимальности решения требуется, чтобы на тех маршрутах, по которым действительно перевозится продукция, его цена в пункте назначения возрастала ровно на цену его перевозки, а в соответствии с условием (3.3) в оптимальном решении цена продукции в пункте назначения не может быть меньше ее цены в пункте отправки с учетом затрат на перевозку.
Сформулированная теорема позволяет построить алгоритм определения оптимального решения транспортной задачи. При реализации такого алгоритма переход из одного базисного решения к следующему осуществляется путем построения цикла и сдвига по нему.
Определение 3.1. «Циклом в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно в строке, другое в столбце. Если ломаная линия пересекается, то точка самопересечения не является вершиной».
Лемма 3.1. «Для любой свободной клетки можно построить только один цикл».
Лемма 3.2. «Переход из одного базисного решения к следующему осуществляется посредством операции сдвига по циклу».
Правило сдвига по циклу:
1) каждой из клеток, связанных циклом с данной свободной клеткой приписывается определенный знак, причем свободной клетке знак +, а всем остальным клеткам поочередно знаки – и +;
2) в данную свободную клетку переносят меньшее из чисел xij, стоящих в минусовых клетках; одновременно это число прибавляют к числам, стоящим в плюсовых клетках и вычитают из чисел в минусовых клетках.
Таким образом меняется свободная клетка и получается новое базисное решение транспортной задачи. При сдвиге число занятых клеток остается постоянным: m + n – 1. Если в минусовых клетках имеется 2 или более одинаковых чисел xij, то освобождается только одна из них, а остальные считаются занятыми (с нулевыми поставками).
Таким образом для решения транспортной задачи методом потенциалов необходимо реализовать следующий укрупненный алгоритм.
Шаг 1. Определение базисного решения из m + n – 1 элементов (например, методом минимальной стоимости).
Шаг 2. В соответствии с условием (3.2) теоремы 3.4 определение потенциалов βj и αi для всех пунктов назначения и отправления.
Шаг 3. Для каждой свободной клетки вычисление числа
γij = βj – αi – cij.
Если все γij ≤ 0, то в соответствии с теоремой 3.4, решение оптимально, если имеются γij > 0, то переход к новому базисному решению.
Шаг 4. Среди положительных γij выбирают максимальное и для свободной клетки, которой оно соответствует, строят цикл пересчета и производят сдвиг по этому циклу. Переход на шаг 2.
Для численной иллюстрации метода потенциалов воспользуемся примером, использованным при рассмотрении метода минимальной стоимости. Базисное решение, найденное в пункте 3.2 равно
x13 = 80; x24 = 10; x33 = 15; x21 = 60; x32 = 25; x34 = 45
и уже записано в табл. 3.2. Поэтому сразу переходим на шаг 2. Для определения значений потенциалов построим систему уравнений:
β3 – α1 = 1; β4 – α2 = 8; β3 – α3 = 3;
β1 – α2 = 4; β2 – α3 = 2; β4 – α3 = 6
содержащую m + n – 1 = 6 уравнений с m + n = 7 неизвестными. Полагая значение одного из потенциалов равным нулю α1 = 0, находим значения всех остальных потенциалов:
α2 = –4; α3 = –2; β1 = 0; β2 = 0; β3 = 1; β4 = 4.
Далее на шаге 3 для каждой свободной клетки вычисляем числа
γ11 = β1 – α1 – c11 = –5; γ22 = β2 – α2 – c22 = –1;
γ12 = β2 – α1 – c12 = –8; γ23 = β3 – α2 – c23 = –4;
γ14 = β4 – α1 – c14 = 2; γ31 = β1 – α3 – c31 = –7.
Так как среди чисел γij имеются положительные, то полученное базисное решение не является оптимальным и необходимо перейти к новому базисному решению. Поэтому на шаге 4 для свободной клетки с наибольшим значением γ14 = 2 строим цикл пересчета (табл. 3.3) и производим сдвиг по этому циклу на наименьшее число в минусовых клетках, равную 45. Клетка в которой находится это число становится
|
5 |
8 |
1 – 80 |
2 + |
80 |
|
4 60 |
6 |
9 |
8 10 |
70 |
|
9 |
2 25 |
3 + 15 |
6 – 45 |
85 60 |
|
60 |
25 |
95 15 |
55 |
|
свободной в новой табл. 3.4.
Таблица 3.4
|
5 |
8 |
1 35 |
2 45 |
80 |
|
4 60 |
6 |
9 |
8 10 |
70 |
|
9 |
2 25 |
3 60 |
6 |
85 |
|
60 |
25 |
95 |
55 |
|
Для полученного нового базисного решения повторим все выкладки шагов 2 и 3. Так на шаге 2 из шести уравнений
β3 – α1 = 1; β1 – α2 = 4; β2 – α3 = 2;
β4 – α1 = 2; β4 – α2 = 8; β3 – α3 = 3
находим:
α1 = 0; α2 = –6; α3 = –2; β1 = –2; β2 = 0; β3 = 1; β4 = 2.
На шаге 3 определяем значения параметров
γ11 = β1 – α1 – c11 = –7; γ22 = β2 – α2 – c22 = 0;
γ12 = β2 – α1 – c12 = –8; γ23 = β3 – α2 – c23 = –2.
Так как все числа γij не положительны, то в соответствии с теоремой 3.4 полученное решение
 f = 675.
f = 675.
оптимально.