Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.1. Постановка задачи и геометрическая интерпретация
Значительное число прикладных задач математического программирования требуют целочисленного решения, например, задачи распределения транспортных средств, производства неделимой продукции и др. Задача целочисленного программирования формулируется также, как и задача математического программирования, но с дополнительным требованием целочисленности переменных. Если это требование относится ко всем переменным, то говорят о полностью целочисленных задачах, в противном случае о частично целочисленных задачах. Учитывая, что наиболее изученными являются целочисленные задачи линейного программирования, в дальнейшем под термином целочисленное программирование будем понимать линейные задачи.
Задача целочисленного программирования в общем случае имеет следующую математическую формулировку:
– найти максимум целевой функции
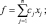(4.1)
– при соблюдениях ограничений
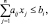i = 1, 2, …, m;
xj ≥ 0; j = 1, 2, …, n,
где xj – целые для j = 1, 2, …, n1. (4.2)
Если n1 < n – частично целочисленная, а при n1 = n – целочисленная задача.
В настоящее время существуют достаточно много методов решения задач целочисленного программирования, которые можно объединить в две группы: методы отсечения и комбинаторные методы. Однако эти методы не обеспечивают желательной эффективности своих вычислительных процедур, что особенно проявляется при увеличении размерности задачи. Но сначала выясним почему нельзя находить решения задачи целочисленного программирования путем округления до ближайших целых чисел решения соответствующей ей задачи линейного программирования. Подтвердим сказанное на конкретном примере:
f = x1 + 3x2 + 3x3 → min;
2x1 + x2 – x3 ≤ 4;
4x1 – 3x2 ≤ 4;
–3x1 + 2x2 + x3 ≤ 3;
xj ≥ 0, xj – целые, j = 1, 2, 3.
Если не учитывать условие целочисленности, то оптимальное решение равно:
x1 = 1/2; x2 = 0; x3 = 4,5; f = 14,
а с учетом целочисленности:
x1 = 2; x2 = 2; x3 = 5; f = 23.
Чтобы понять суть этой проблемы обратимся к геометрической иллюстрации отличий областей допустимых решений задачи линейного программирования и задачи целочисленного программирования.
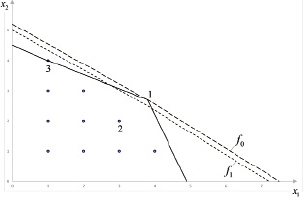
Рис. 4.1. Области допустимых решений ЗЛП и ЦП
Как видно из рис. 4.1 оптимальное решение задачи линейного программирования расположена в точке 1. При округлении значения этого решения получим точку 2, которая очень далека от оптимального целочисленного решения в точке 3 [19].