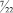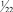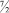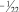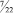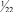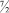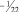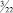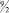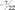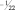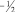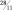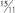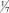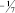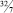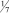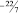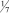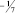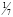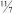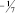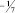Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные методы оптимизации

Шукаев Д. Н.,

4.2.1. Метод Р. Гомори

Этот метод применяется для решения задачи целочисленного программирования (4.1), (4.2), при условии целочисленности всех коэффициентов и правых частей ограничений задачи. Эти условия не сужают область применения метода, так как вполне выполнимы. Например, [37], ограничение

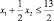
легко можно записать в виде неравенства

6x1 + 2x2 ≤ 39,

в которой дроби отсутствуют.

Необходимость введения требования целочисленности параметров исходной задачи обусловлена следующими соображениями. Из дальнейшего рассмотрения будет видно, что как исходные, так и дополнительные переменные задачи, решаемые методом Р. Гомори, должны быть целочисленными. Между тем, наличие в ограничениях дробных коэффициентов приводит к нарушению целочисленности дополнительных переменных.

Перейдем к рассмотрению сути метода. На первом этапе решается задача с ослабленными ограничениями, не содержащими условия целочисленности переменных. Если полученное оптимальное решение оказывается целочисленным, то оно является также решением исходной задачи. В противном случае необходимо ввести дополнительные ограничения, порождающие, вместе с исходными ограничениями, новую задачу линейного программирования, решение которой оказывается целочисленным и совпадает с оптимальным решением исходной целочисленной задачи. Пусть последняя симплексная таблица задачи с ослабленными ограничениями имеет следующий вид:

Таблица 4.1

Базисн. перем.	x1	…	xi0	…	xm	V1		Vj		Vn	Решение
x1	1	…	0	…	0	a11	…	a1j	…	a1n	b1
...	...										....
xi	0	…	1	…	0	ai1	…	aij	…	ain	bi
....	....										....
xm	0	…	0	…	1	am1	…	amj	…	amn	bm
f	0	…	0	…	0	c1	…	cj	…	cn	f0

 

Здесь x_i (i = 1, 2, …, m) – базисные переменные, а v_j (j = 1, 2, …, n) – небазисные переменные.

Пусть i-я строка таблицы соответствует нецелому значению базисной переменной xi. Выразим эту переменную как

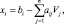(4.3)

где bi – нецелое число. Далее представим правые части в виде

b_i = [b_i] + d_i; (4.4)

a_ij = [a_ij] + d_ij, (4.5)

где в квадратных скобках записано наибольшее целое число, которое меньше, чем число внутри скобки. Например, если

b1 = 3/2, то [b1] = 1, а di = 1/2

или если

a11 = –5/2, то [d11] = –3, а d11 = 2/3.

После подстановки (4.4) и (4.5) в (4.3) получим

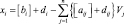
или

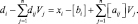(4.6)

Поскольку все переменные xi и vj принимают целые значения, правая часть выражения (4.6) должна быть целочисленной, откуда следует, что левая часть этого выражения также должна принимать целые значения. Далее, так как

d_ij ≥ 0 и Vj ≥ 0

для всех i и j, то

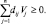
Следовательно, выполняется неравенство

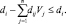
Это означает, что

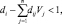
поскольку di < 1.

Так как левая часть этого неравенства должна принимать целые значения, можно записать необходимое условие ее целочисленности как

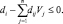
Это ограничение перепишем в виде равенства

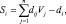(4.7)

где Si – неотрицательная дополнительная переменная, которая по определению должна принимать целые значения.

Такое ограничение-равенство определяет отсечение Гомори для полностью целочисленной задачи.

Из симплексной таблицы следует, что vj = 0 и, следовательно Si = –di, то есть данная компонента решения не является допустимой. Это означает, что полученное ранее решение непрерывной задачи не удовлетворяет новому ограничению.

В такой ситуации следует использовать двойственный симплекс-метод (раздел 2.5), реализация которого обеспечивает отсечение некоторой области многогранника решений, не содержащих точек с целочисленными координатами.

Преобразуем исходную табл. 4.1 путем приписывания к ней строки и столбца, соответствующих построенному отсечению Гомори для полностью целочисленной задачи. В результате получим новую табл. 4.2.

Таблица 4.2

Базисн. перем.

x1

…

xi

…

xm

V1

Vj

Vn

Si

Решение

x1

1

…

0

…

0

a11

…

a1j

…

a1n

0

b1

...

...

...

...

xi

0

…

1

…

0

ai1

…

aij

…

ain

0

bi

...

...

...

...

xm

0

…

0

…

1

am1

…

amj

…

amn

0

bm

f

0

…

0

…

0

c1

…

cj

…

cn

0

f0

Si

0

…

0

…

0

–di1

…

–dij

…

–din

1

–di

 

Если полученное (в результате применения двойственного симплекс-метода) решение является целочисленным, то процесс решения исходной задачи завершен. В противном случае необходимо ввести новое отсечение на базе полученной табл. 4.2 и вновь воспользоваться двойственным симплекс-методом. Эта процедура повторяется до тех пор, пока не будет найдено целочисленное решение.

Если на некоторой итерации при использовании двойственного симплекс-метода обнаруживается отсутствие допустимого решения, то рассматриваемая задача не имеет допустимого решения.

При знакомстве с методом Гомори может сложится впечатление, что размеры симплекс-таблицы неограниченно возрастают по мере добавления новых отсечений. Это не соответствует действительности. Общее число ограничений порожденной задачи не может превышать количества переменных исходной задачи [37].

Таким образом, описанные процедуры решения целочисленной задачи линейного программирования можно формализовать в виде следующего алгоритма.

Шаг 1. Решается исходная целочисленная задача линейного программирования с ослабленным ограничением, то есть без требования целочисленности оптимальных решений, отображаемых в итоговой симплекс-табл. 4.1.

Шаг 2. Проверяется целочисленность оптимальных решений. Если в столбце решений итоговой симплекс-таблицу (табл. 4.1) содержатся только целые числа, то получено оптимальное решение целочисленной задачи линейного программирования. В противном случае переход на шаг 3.

Шаг 3. Если в столбце решений содержаться дробные решения, то для выбранного дробного решения формируется уравнение отсечения Гомори (4.7) и это уравнение добавляется в систему ограничений исходной задачи в виде дополнительной Si – строки итоговой таблицы шага 1.

Шаг 4. С помощью алгоритма двойственного симплекс-метода осуществляется переход к следующей симплекс-таблице. Далее возврат на шаг 2.

Метод Гомори имеет два недостатка. Первое – ошибки округления, возникающие в процессе вычислений на компьютере, в ряде случаев, приводят к получению неверного (неоптимального) целочисленного решения. Второе – решения, последовательно получаемые в процессе реализации метода, не являются допустимыми, то есть алгоритм не позволяет получить какое-либо целочисленное решение, отличное от оптимального. Это означает, что в случае вынужденного прекращения вычислений до момента окончания процесса решения в памяти компьютера не будет содержаться никакого «приемлемого» целочисленного решения исходной задачи.

Пример 4.1. Пусть необходимо максимизировать функцию

f = 7x1 + 9x2 → max, (4.7)

при ограничениях

–x1 + 3x₂ ≤ 6;

7x1 + x₂ ≤ 35;

x1 ≥ 0; x2 ≥ 0, (4.8)

x1 и x2 – целые. (4.9)

Шаг 1. Решаем исходную задачу без учета ограничения (4.9). Применяя обычный симплекс-алгоритм (раздел 2.3) получим следующую итоговую симплекс-таблицу (табл. 4.3).

Таблица 4.3

БП	x1	x2	x3	x4	Решение
x2	0	1
x1	1	0
f	0	0			63

 

Шаг 2. Полученное оптимальное решение задачи линейного программирования является дробным:

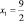и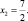

Переход на шаг 3.

Шаг 3. Учитывая, что 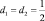в качестве производящей строки можно выбрать любую из двух строк таблицы. Выберем строку соответствующей переменной x2:

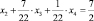
или

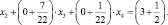
Следовательно, уравнение отсечения Гомори имеет вид

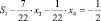
и определяет дополнительную Si – строку в новой симплекс-таблице (табл. 4.4).

Таблица 4.4

БП	x1	x2	x3	x4	S1	Правая часть
x2	0	1			0
x1	1	0			0
S1	0	0			1
f	0	0			0	63

Шаг 4. С помощью алгоритма двойственного симплекс-метода осуществляется переход к следующей симплекс-таблице (табл. 4.5).

Таблица 4.5

БП	x1	x2	x3	x4	S1	Решение
x2	0	1	0	0	1	3
x1	1	0	0
x3	0	0	1
f	0	0	0	1	8	59

которая также не приводит (шаг 2) к оптимальному целочисленному решению. Поэтому на шаге 3 формируем новое отсекающее уравнение Гомори. В табл. 4.5 строке с базисной переменной x1 соответствует равенство

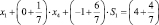
порождающее отсечение

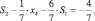
Добавим это отсечение к последней таблице

Таблица 4.6

БП	x1	x2	x3	x4	S1	S2	Решение
x2	0	1	0	0	1	0	3
x1	1	0	0			0
x3	0	0	1			0
S2	0	0	0			1
f	0	0	0	1	8	0	59

И в результате повторного использования (шаг 4) двойственного симплекс-метода получим табл. 4.7, которая дает оптимальное целочисленное решение исходной задачи:

x1 = 4; x2 = 3; f = 55.

Таблица 4.7

БП	x1	x2	x3	x4	S1	S2	Решение
x2	0	2	0	0	1	0	3
x1	1	0	0	0	–1	1	4
x3	0	0	1	0	–4	1	1
x4	0	0	0	1	6	–7	4
f	0	0	0	1	2	7	55

Геометрическая интерпретация данного примера наглядно демонстрирует (рис. 4.2) как рассмотренные выше дополнительные отсечения исключают некоторые области многогранника допустимых решений [37]. Первое отсечение

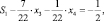
записанное в переменных x1 и x2, после соответствующей замены принимает следующий вид

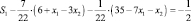
или S1 + x2 = 3.

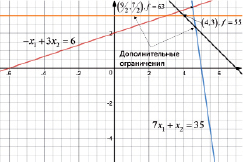
Рис. 4.2. Области допустимых решений непрерывной и целочисленной задач

Это уравнение эквивалентно неравенству x₂ ≤ 3.

Аналогичным образом второе отсечение

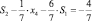
порождает эквивалентное ограничение в переменных x1 и x2:

x1 + x2 ≤ 7.

На рис. 4.2 показано, как введение этих двух ограничений позволяет получить новую экстремальную точку с координатами (4, 3), в которой достигается оптимум исходной целочисленной задачи.