
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.2.1. Метод ветвей и границ
Рассмотрим принцип действия этого метода. Как и в методе Гомори здесь также вначале решается задача без учета условия целочисленности. Пусть x* дробное решение этой задачи. Интервал [37]
[x*] < x < [x*] + 1,
где квадратная скобка означает операцию выделения целой части, не содержит допустимых целочисленных компонент решения. Поэтому допустимое целое значение должно удовлетворять одному из неравенств
x ≤ [x*] или x ≥ [x*] + 1.
Введение этих условий в задачу с ослабленными ограничениями (т.е. без учета целочисленности) порождает две не связанные между собой задачи. Таким образом исходная задача разветвляется на две подзадачи. Осуществляемый в процессе ветвления (рис. 4.3) учет необходимых условий целочисленности позволяет исключить части многогранника допустимых решений, не содержащие точек с целыми координатами. Затем каждая подзадача решается как задача линейного программирования с целевой функцией исходной задачи. Если полученное решение оказывается допустимым для целочисленной задачи, то оно и будет оптимальным и нет необходимости продолжать «ветвление» подзадачи. В противном случае подзадача в свою очередь должна быть разбита на две подзадачи опять при учете условия целочисленности переменных, значения которых в оптимальном решении не являются целыми. Как только полученное допустимое целочисленное решение одной из подзадач оказывается имеющегося, оно фиксируется вместо зафиксированного ранее. Процесс ветвления продолжается, насколько это возможно, до тех пор, пока каждая подзадача не приведет к целочисленному решению или пока не будет установлена невозможность улучшения имеющегося решения. В этом случае зафиксированное допустимое решение является оптимальным.
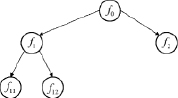
Рис. 4.3. Схема ветвления
С учетом сказанного можно построить следующий укрупненный алгоритм метода ветвей и границ.
Шаг 1. Решить задачу целочисленного программирования без учета целочисленности переменных.
Шаг 2. Проверить все ли решения целые:
а) если да, то найдено оптимальное решение;
б) если нет, перейти на следующий шаг.
Шаг 3. Выбрать любое нецелое решение, округлить до ближайшего целого в меньшую и большую сторону 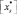 и
и 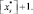
Шаг 4. Решить полученные две подзадачи
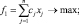
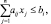 i = 1, 2, …, m;
i = 1, 2, …, m;
xj ≥ 0, j = 1, 2, …, n;
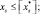
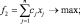
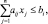 i = 1, 2, …, m;
i = 1, 2, …, m;
xj ≥ 0, j = 1, 2, …, n;
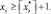
Шаг 5. Выбрать точку ветвления по наилучшему значению целевой функции среди висячих вершин дерева ветвления.
Шаг 6. Проверка для выбранной точки ветвления все ли 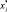 – целые:
– целые:
а) если да, то получено оптимальное решение;
б) если нет, то переход на шаг 3.
Пример 4.2.
f = x1 + x2 → max;
2x1 + 11x2 ≤ 38;
x1 + x2 ≤ 7;
4x1 – 5x2 ≤ 5;
x1 ≥ 0, x2 ≥ 0, xj – целые.
Шаг 1. Решение задачи без учета условия целочисленности
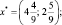 f0 = 7.
f0 = 7.
Шаг 2. Оптимального целочисленного решения нет. Переход на шаг 3.
Шаг 3. Выбираем переменную 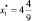 .
.
Шаг 4. Решаем две задачи
|
f1 = x1 + x2 → max, 2x1 + 11x2 ≤ 38; x1 + x2 ≤ 7; 4x1 – 5x2 ≤ 5; x1 ≤ 4; xj ≥ 0. |
f2 = x1 + x2 → max, 2x1 + 11x2 ≤ 38; x1 + x2 ≤ 7; 4x1 – 5x2 ≤ 5; x1 ≥ 5; xj ≥ 0. |
Решение
|
|
Допустимого решения нет f2 = –∞ |
Шаг 5. Выбираем узел ветвления f1.
Шаг 6. Оптимального целочисленного решения нет. Переход на шаг 3.
Шаг 3. Выбираем переменную 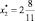 .
.
Шаг 4. Решаем две подзадачи
|
f11 = x1 + x2 → max, 2x1 + 11x2 ≤ 38; x1 + x2 ≤ 7; 4x1 – 5x2 ≤ 5; x2 ≤ 2; xj ≥ 0. Решение: x = (3,75; 2) f11 = 5,75. |
f12 = x1 + x2 → max, 2x1 + 11x2 ≤ 38; x1 + x2 ≤ 7; 4x1 – 5x2 ≤ 5; x2 ≥ 3; xj ≥ 0. Решение: x = (2,5; 3) f12 = 5,5. |
Шаг 5. Выбираем узел ветвления f11.
Шаг 4. Решаем две подзадачи.
|
f111 = x1 + x2 → max, 2x1 + 11x2 ≤ 38; x1 + x2 ≤ 7; 4x1 – 5x2 ≤ 5; x1 ≤ 3; xj ≥ 0. Решение: x = (3; 2); f = 5. |
f112 = x1 + x2→max, 2x1 + 11x2 ≤ 38; x1 + x2 ≤ 7; x1 + x2 ≤ 7; 4x1 – 5x2 ≤ 5; x1 ≥ 4; xj ≥ 0. Решения нет |
Находим оптимальное решение
x1 = 3; x2 = 2; f = 5.

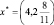 ;
;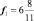 .
.