
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.1. Постановка и основные положения задачи нелинейного программирования
Нелинейное программирование – это направление математического программирования, предназначенное для решения оптимизационных задач, когда целевая функция и ограничивающие условия не обязательно линейны.
Наиболее употребляемая запись задачи нелинейного программирования имеет вид:
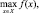 (5.1)
(5.1)
где X = {x/g(x) ≤ b, x ≥ 0}.
Для такой общей постановки задачи нелинейного программирования не существует универсальных методов ее решения. Однако для отдельных классов задач нелинейного программирования (выпуклое или квадратичное программирование) с дополнительными условиями относительно свойств функций f(x) и g(x) разработаны эффективные методы их решения.
Как было показано ранее в разделе, посвященной методам классической оптимизации, при решении оптимизационных задач важно иметь необходимые условия, которым должно удовлетворять решение, оптимизирующее целевую функцию при заданных ограничениях. Хотя такие условия обычно не являются достаточными, но знание их существенно облегчает поиск оптимального решения. Так в классической задаче безусловной оптимизации необходимыми условиями оптимума являются условия (1.14), определяющие стационарные точки целевой функции f(x). В задачах нелинейного программирования аналогичными условиями являются условия Куна-Таккера, вытекающие из теоремы Куна – Таккера. Эта теорема является одной из наиболее важных теорем математического программирования и служит основой многих вычислительных алгоритмов. Прежде чем сформулировать эти условия введем ряд новых понятий в дополнение к тем, которые были введены в начале этой книги (раздел В1).
Определение 5.1 [2]. Множество допустимых решений Х задачи (5.1) удовлетворяет условию регулярности, если существует хотя бы одна точка x ∈ X такая, что g(x) < b.
Определение 5.2. Задача (5.1) называется задачей выпуклого программирования, если функция f(x) является вогнутой (выпуклой), а функции g(x) выпуклыми.
Определение 5.3. Функцией Лагранжа задачи выпуклого программирования называется функция
L(x, y) = f(x) + y[b – g(x)],
где у – вектор множителей Лагранжа. В скалярной форме
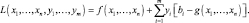
Определение 5.4. Точка (x*, y*) называется седловой точкой функции Лагранжа, если
L(x, y*) ≤ L(x*, y*) ≤ L(x*, y)
для всех x ≥ 0 и y ≥ 0.
Теорема 5.1 (теорема Куна – Таккера). «Для задачи выпуклого программирования множество допустимых решений Х которой обладает свойством регулярности, x* является оптимальным решением тогда и только тогда, когда существует такой вектор y* ≥ 0, что (x*, y*) – седловая точка функции Лагранжа».
Если f(x) и g(x) непрерывно дифференцируемы, тогда теорему можно дополнить следующими условиями Куна – Таккера, определяющими необходимые и достаточные условия, чтобы (x*, y*) была седловой точкой функции Лагранжа, а следовательно по теореме Куна – Таккера и решением задачи выпуклого программирования:
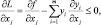 j = 1, …, n;
j = 1, …, n;
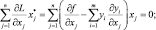
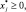 j = 1, …, n; (5.2)
j = 1, …, n; (5.2)
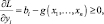 i = 1, …, m;
i = 1, …, m;
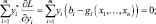
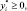 i = 1, …, m,
i = 1, …, m,
где все переменные, функции и производные вычисляются в седловой точке.
Типичной задачей выпуклого программирования является задача квадратичного программирования
f(x) = cx + xTDx;
Ax ≤ b;
x ≥ 0
или в скалярной форме
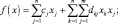
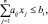 i = 1, …, m,
i = 1, …, m,
xj ≥ 0, j = 1, …, n. (5.3)
Здесь 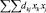 – отрицательно (положительно) полуопределенная квадратичная функция.
– отрицательно (положительно) полуопределенная квадратичная функция.
Определение 5.5. Квадратичная функция является вогнутой, если она отрицательно полуопределена 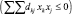 и выпуклой, если она положительно полуопределена
и выпуклой, если она положительно полуопределена 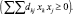
Для сформулированной задачи квадратичного программирования построим функцию Лагранжа
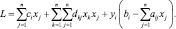
Если L имеет седловую точку (x*, y*), то в этой точке выполняются условия Куна – Таккера (5.2). Приведем первую и четвертую неравенства условия Куна – Таккера в равенства
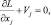 j = 1, …, n; (5.4)
j = 1, …, n; (5.4)
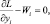 i = 1, …, m; (5.5)
i = 1, …, m; (5.5)
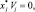 j = 1, …, n; (5.6)
j = 1, …, n; (5.6)
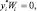 i = 1, …, n; (5.7)
i = 1, …, n; (5.7)
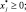 Vj ≥ 0;
Vj ≥ 0; 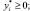 Wi ≥ 0; (5.8)
Wi ≥ 0; (5.8)
(j = 1, …, n, i = 1, …, m)
Таким образом, чтобы найти решение задачи квадратичного программирования (5.3) нужно определить неотрицательное решение системы линейных уравнений (5.4) и (5.5), удовлетворяющих условиям (5.6) и (5.7). Для этого надо решить задачу линейного программирования
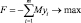 ;
;
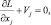 j = 1, …, n;
j = 1, …, n;
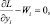 i= 1, …, m,
i= 1, …, m,
с учетом условий (5.6) и (5.7). Здесь yi – искусственные переменные, введенные в уравнения (5.4) и (5.5). Таким образом процесс решения задачи квадратичного программирования состоит из четырех этапов.
Этап 1. Составление функции Лагранжа.
Этап 2. Определения условий (5.4)–(5.8) существования седловой точки для функции Лагранжа.
Этап 3. С помощью метода искусственного базиса определение координаты седловой точки.
Этап 4. Принятие седловой точки за оптимальное решение и вычисление значения целевой функции.
Пример 5.1 [2].
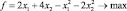 ;
;
x1 + 2x2 ≤ 8;
2x1 – x2 ≤ 12;
x1, x2 ≥ 0.
Решение. Целевая функция вогнута, так как является суммой линейной функции (которую можно рассматривать как вогнутую) и квадратичной формы, которая является отрицательно – определенной и, следовательно, вогнутой. Ограничения линейны, поэтому можно воспользоваться теоремой Куна – Таккера.
Построим функцию Лагранжа (этап 1)
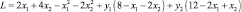
и необходимые и достаточные условия (5.4)–(5.8) существования седловой точки для функции Лагранжа (этап 2)
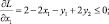
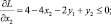
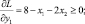
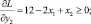 (5.9)
(5.9)
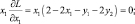
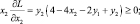
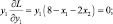
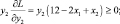
y1 > 0, y2 > 0, x1 ≥ 0, x2 ≥ 0. (5.10)
Систему неравенств (5.9) перепишем в виде
2x1 + y1 + 2y2 ≥ 2;
4x2 + 2y1 – y2 ≥ 4;
x1 + 2x2 ≤ 8;
2x1 – x2 ≤ 12.
Введя дополнительные неотрицательные переменные V1, V2, W1, W2 получим
2x1 + y1 + 2y2 – V1 = 2;
4x2 + 2y1 – y2 – V2 = 4;
x1 + 2x2 + W1 = 8;
2x1 – x2 + W2 = 12. (5.11)
Далее запишем
V1x1 = 0; V2x2 = 0; W1y1 = 0; W2y2 = 0. (5.12)
Если теперь найти базисное решение системы линейных уравнений (5.11), то будет получена седловая точка функции Лагранжа для исходной задачи, т.е. определено оптимальное решение.
Для определения на этапе 3 базисного решения системы линейных уравнений (5.11) воспользуемся методом искусственного базиса [2]. В первое и второе уравнения добавим дополнительную неотрицательную переменную z1 и z2 и решим задачу линейного программирования
F = –Mz1 – Mz2 > max;
2x1 + y1 + 2y2 – V1 + z1 = 2;
4x2 + 2y1 – y2 – V2 + z2 = 4;
x1 + 2x2 + W1 = 8;
2x1 – x2 + W2 = 12
при всех x, y, V, W, z ≥ 0.
Оптимальное решение равно
x1 = 1, x2 = 1,
w1 = 5, w2 = 11, остальные переменные = 0.
Проверив условия (5.12) убеждаемся, что решение
(x*, y*) = (1, 1, 0, 0)
действительно является седловой точкой функции Лагранжа для исходной задачи.
Таким образом x* = (1; 1) – оптимальное решение исходной задачи и fmax = 3.
