
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.2. Градиентные методы
В основу градиентных методов определения оптимума положены вычисление и анализ производных целевой функции задачи нелинейного программирования. Поэтому целевые функции таких задач должны быть как минимум дважды дифференцируемы. Суть метода заключается в построении последовательности точек, которая начинается с заданной исходной точки xk в направлении наискорейшего увеличения целевой функции (в задаче максимизации) и завершается определением оптимального или приемлемого решения исходной задачи. Такой метод называется градиентным, так как градиент целевой функции
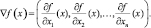
вычисленный в некоторой точке, указывает направление максимального возрастания этой функции. Использование градиентных методов для решения задач нелинейного программирования в общем случае позволяет найти точку локального оптимума. Глобальный оптимум можно найти только в задачах, целевая функция которых является вогнутой (выпуклой), а область допустимых решений выпуклой. Существуют две группы градиентных методов. К первой группе относятся методы, исследуемые точки которых находятся в допустимой области решения, например, метод Франка-Вульфа. Ко второй группе относятся методы, где это условие необязательно, кроме конечной точки. Здесь наибольшее распространение получил метод штрафных функций.
При применении градиентных методов итерационный процесс продолжается до тех пор, пока градиент целевой функции в очередной точке xk+1 не станет равным нулю или же пока
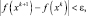
где ε– заданная точность решения.
