
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.1. Понятие и суть динамического программирования
В предыдущих разделах были рассмотрены одношаговые или одноэтапные методы оптимизации. Теперь перейдем к многошаговым методам оптимизации. Одним из наиболее известных многошаговых методов оптимизации является динамическое программирование, предложенное в пятидесятые годы прошлого века американским ученым Ричардом Беллманом. Динамическое программирование можно определить, как набор математических процедур, используемых при анализе многошаговых процессов принятия решений [17]. В свою очередь многошаговый процесс принятия решений можно определить, как деятельность, при которой принимаются последовательные решения, направленные на достижение единой цели.
Суть динамического программирования заложено в принципе оптимальности, которая звучит так – оптимальная стратегия обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальную стратегию относительно состояния, возникающего после первого решения [3].
Многошаговые процессы принятия решений встречаются в самых различных ситуациях, например, в задачах управления запасами, при распределении ресурсов или управлении космическим аппаратом. Каждый многошаговый процесс принятия решений интуитивно можно считать, как развитием наиболее понятного многошагового процесса нахождения кратчайшего пути в направленной сети (рис. 6.1). На этом примере можно наиболее наглядно продемонстрировать и суть самого принципа оптимальности Р. Беллмана.
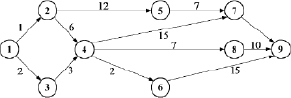
Рис. 6.1. Направленная сеть
Пусть направленная сеть имеет N этапов принятия решений. Из визуального анализа сети, изображенной на рис. 6.1 можно принять N = 5. Введем следующие обозначения:
n – номер этапа (n = 1, 2, 3, 4,5 );
i – пункт, откуда осуществляется движение (i = 1, 2, …, 8);
j – пункт, в который направлено движение (j = 2, 3, …, 9);
sij – расстояние из пункта i в пункт j;
Sn(i) – минимальное расстояние на n-м этапе решения задачи из пункта i до конечного пункта.
Будем считать, что пункт принадлежит n-му этапу, если из него можно попасть в конечный пункт ровно за n этапов.
Очевидно, что минимальный путь из пункта n-го этапа до конечного пункта 9 будет зависеть от того, в каком пункте этого этапа мы окажемся. Номер i пункта, принадлежащего n-му этапу, будет являться переменной состояния системы на n-м этапе. Поскольку оптимизация обычно начинается с конца процесса, то, находясь в некотором пункте i n-го этапа, принимается решение о переходе в один из пунктов (n – 1)-го этапа, а направление дальнейшего движения известно из предыдущих этапов. Номер j пункта (n – 1)-го этапа будет переменной управления на n-м этапе.
Для первого этапа (n = 1) целевая функция (функция Беллмана) представляет собой минимальный путь из пунктов первого этапа (6, 7, 8) в конечный пункт 9, т.е. S1(i) = si9. Для последующих этапов длина пути складываются из двух слагаемых – пути sij из пункта i n-го этапа в пункт j (n – 1)-го этапа и минимально возможной длины пути из пункта j до конечного пункта, т.е. Sn–1(j). Таким образом, функциональное уравнение Беллмана будет иметь вид
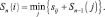
Минимальная длина достигается на некотором значении j*, которое является оптимальным направлением движения из пункта i в конечный пункт.
На пятом этапе попадаем на исходный пункт и состояние системы становится определенным i = 1. Функция S5(1) представляет собой минимально возможный путь из 1-го пункта в 9-й пункт. Оптимальный маршрут определяется в результате анализа всех этапов в обратном порядке.
Проиллюстрируем этот пример по конкретным значениям длин дуг, показанных на рис. 6.1.
Пример 6.1. Алгоритм определения кратчайшего пути состоит из следующих шагов.
Шаг 1. n = 1, S1(i) = si9. На первом этапе в пункт 9 можно попасть из пунктов 6, 7, 8 второго этапа. Следовательно: S1(6) = 15; S1(7) = 3; S1(8) = 10.
Шаг 2. n = 2, здесь рассматриваем пути из пунктов (4 и 5) третьего этапа в пункты второго этапа. Функциональное уравнение Беллмана здесь имеет вид:
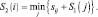
Cледовательно, имеем:
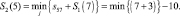
Условно оптимальный путь (5–7);
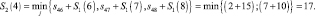
Условно оптимальные пути (4–6 и 4–8).
Шаг 3. n = 3, здесь рассматриваем пути из пунктов (2 и 3) четвертого этапа в пункты третьего этапа.
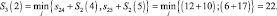
Условно оптимальный путь (2–5).
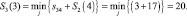
Условно оптимальный путь (3–4).
Шаг 4. n = 4, здесь рассматриваем пути из начального пункта 1 в пункты четвертого этапа.
S4(1) = min{s12 + S3(2), s13 + S3(3)} = min{(1 + 22); (2 + 20);} = 22.
Условно оптимальный путь (1–3).
Теперь найдем безусловный кратчайший путь от пункта 1 до пункта 9. На этапе условной оптимизации получено, что минимальный путь имеет длину S4(1) = 22. Этот результат достигается при движении из первого пункта в третий, затем необходимо двигаться в четвертый. Из этого пункта, как показано на шаге 2 возможно два равнозначных направления в пункты 6 и 7. Таким образом, оптимальное решение достигается двумя маршрутами, показанными на рис. 6.2, а именно (1–3–4–6–9) и (1–3–4–8–9).
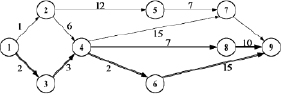
Рис. 6.2. Оптимальный путь
