Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные методы оптимизации

Шукаев Д. Н.,

6.2. Метод функциональных уравнений

Как показал Р. Беллман [3], определение оптимального решения многоэтапного процесса сводится к использованию некоторого функционального уравнения, основанного на принципе оптимальности Беллмана. Для построения такого уравнения рассмотрим следующую задачу математического программирования

W = g1(x1) + g2(x2) + … + g_n(x_n); 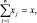x_j ≥ 0, i = 1, …, n. (6.1)

относящейся к классу задач распределения ресурсов. Эта задача имеет аддитивную целевую функцию и несмотря на простую структуру может быть решена аппаратом нелинейного программирования в виде статической (одноэтапной) задачи, если только функции gi(x) являются вогнутыми (выпуклыми). Как будет показано ниже, применение для решения таких задач метода функциональных уравнений, в большинстве случаев, позволяет преодолеть различные трудности, связанные с видом их целевых функций.

Поэтому вместо одной задачи (6.1) с заданным количеством ресурсов х и фиксированным числом процессов n рассмотрим целое семейство таких задач, в которых х может принимать любые положительные значения, а n – любые целые значения.

То, что на первый взгляд может показаться статическим процессом необходимо искусственно развернуть во времени и производить распределения ресурсов в каждую единицу времени. Сначало какое-то количество ресурсов назначается n-му процессу, затем (n – 1)-му процессу и т.д. Поступая таким образом вводим динамический процесс распределения.

Перейдем теперь к аналитическому рассмотрению. Так как максимум F зависит от х и n сделаем эту зависимость явной, задав последовательность функций {fn(x)}, определенных для n = 1, 2,…, х, следующим образом

fn(x) = max W(x1, x2, …, xn),

где x_j ≥ 0 и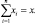

Функция fn(x) выражает оптимальный доход, который получается от распределения ресурсов х по n процессам. В двух частных случаях элементы последовательности {fn(x)} принимают особенно простой вид. Очевидно,

fn(0) = 0, n = 1, 2, …

если gi(0) = 0 для любого i, что является разумным предположением. Также очевидно,

f1(x) = g1(x) (6.2)

для х ≥ 0.

Легко найти рекуррентное соотношение, связывающее fn(x) и fn–1(x) для произвольных n и х. Пусть xn, где 0 ≤ x_n ≤ x – количество ресурсов, назначенных для n-го процесса. Тогда, каково бы ни было значение xn, остающееся количество ресурсов (x – x_n) должно быть использовано так, чтобы получить максимальный доход от оставшихся n – 1 процессов.

Так как этот оптимальный доход от распределения количества ресурсов (x – xn) по n – 1 процессам по определению есть fn–1(x – xn), назначение xn для n-го процесса приводит к общему доходу

g_n(x_n) + f_n–1(x – x_n)

для системы с n процессами.

Ясно, что оптимальным будет такой выбор xn, который максимизирует эту функцию. Таким образом, получаем основное функциональное уравнение Беллмана:

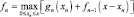(6.3)

для n = 2, 3, ……. Причем f1(x) определяется из выражения (6.2).

Применим метод функциональных уравнений для распределения средств х между двумя предприятиями. Если в первое предприятие вложить средства у, а во второе (х – у), то доходы составят g(y) и h(x – y). Надо так распределить х, чтобы общий доход за первый этап был максимальным

W1(x, y) = g(y) + h(x – y)

для всех y ∈ [0; x].

Рассмотрим двухэтапный процесс. Предположим, что за счет издержек, необходимых для получения дохода g(y) средство у уменьшиться до величины ау, где а < 1. Аналогично (х – у) уменьшиться до величины b(х – у), где b < 1. Так что после первого этапа останется средств

x1 = ay + b(x – y).

Повторим распределение средств

x1 = y1 + (x1 – y1).

Тогда на втором этапе получим доход

g(y1) + h(x1 – y1)

и полный доход будет

;

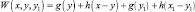W(x, y, y1) = g(y) + h(x – y) + g(y1) + h(x1 – y1),

при 0 ≤ y ≤ x, 0 ≤y1 ≤ x1.

Рассмотрим теперь n этапный процесс

+

;

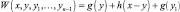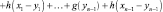W(x, y, y1, …, yn–1 = g(y) + h(x – y) + g(y1) + + h(x1 – y1) + … + g(yn–1) + h(xn–1 – yn–1),

где

x1 = ay + b(x – y);

x2 = ay1 + b(x1 – y1);

…………………;

xn–1 = ayn–2 + b(xn–2 – yn–2).

Прямое решение такой задачи связано со значительными трудностями и как было отмечено выше дает только локальный экстремум. Решим эту задачу поэтапно, основываясь на принципе оптимальности Беллмана. Построим функциональное уравнение для определения максимума функции

fn(x) = max Wn(x, y, y1, …, yn–1)

как рекуррентное соотношение.

Сначала рассмотрим двухэтапный процесс

f2(x) = max {g(y) + h(x – y) + f1[ay + b(x – y)]}= = max {W1(x, y) + f1[ay + b(x – y)]}.

Рассуждая аналогично, получим основное функциональное уравнение для n этапов

fn(x) = max {g(y) + h(x – y) + fn–1[ay + b(x – y)]}= = max {W1(x, y) + fn–1[ay + b(x – y)]}.

Это уравнение позволяет одну n-мерную задачу привести к последовательности n одномерных задач.

Пример 6.2 [7]. Для развития двух предприятий на пять лет выделено х средств. Количество средств, выделенных для первого предприятия (у) дает годовой доход g(y) = y2 и уменьшиться до величины g(y) = 0,75y.

А для второго предприятия, соответственно

h(x – y) = 2(x – y)2 и ρ(x – y) = 0,3(x – y).

Надо максимизировать полный доход за 5 лет (этапов).

Нахождение оптимального решения начинается с пятого этапа, в начале которого надо распределить остаток средств x4. Для этого необходимо определить оптимальное значение y5. Так как

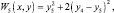
то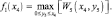

Взяв первую производные от W5 получим

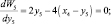
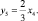
Вторая производная

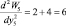
больше нуля и найденное решение соответствует минимуму, а оптимальное решение будет на границе, т.е. y5 = 0. Тогда условный максимальный доход за один пятый год будет

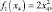
т.е. все оставшиеся средства выделяются на второе предприятие.

Теперь перейдем на четвертый этап, оптимизирующий доход за два последних года

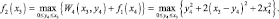
Здесь x4 сумма оставшихся средств после четвертого этапа

x4 = 0,75y4 + 0,3(x3 – y4).

Тогда функциональное уравнение примет вид

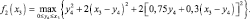
Взяв производную из выражения в фигурной скобке найдем

x4 = 0,75x3.

Вторая производная здесь также указывает на минимум и оптимальное решение снова лежит на концах интервала [0; x3], т.е. все средства в начале четвертого этапа также выделяются второму предприятию и y4 = 0

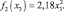
Напишем функциональное уравнение для третьего этапа, где f3(x2) – максимальный доход за последние три года

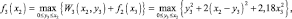
где x3 = 0,75y3 + 0,3(x2 – y3).

Поступая аналогично предыдущим операциям найдем, что оптимальное решение будет

y3 = x2 и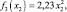

т.е. средства выделяются первому предприятию.

Функциональное уравнение для второго этапа будет

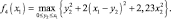
Здесь также средства выделяются первому предприятию y2 = x1 и .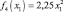

Наконец составляем функциональное уравнение для первого этапа

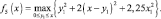
Здесь оптимальное решение y1 = x, т.е. все средства передаются первому предприятию.

Таким образом, оптимальная стратегия состоит в том, чтобы первые три года средства выделялись только первому предприятию, а два последних года – второму предприятию. При этом максимальный доход за пять лет составит

f5(x) = 2,27x².