
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.3. Выбор стратегии обновления оборудования
Одной из важных экономических проблем является своевременное обновление оборудования: станков, транспортных средств, производственных линий и т.д. Решение о замене некоторого оборудования определяется производительностью этого оборудования, эксплуатационными расходами, его остаточной (ликвидной) стоимостью, которая зависит от возраста и стоимостью нового оборудования. Задача заключается в определении оптимальных сроков замены старого оборудования некоторого предприятия.
Построим модель такой задачи. Критерием оптимальности являются либо максимизация дохода от эксплуатации оборудования, либо минимизация суммарных затрат на эксплуатацию в течение планируемого периода.
Пусть r(t) доход от эксплуатации единицы оборудования в возрасте t лет в течение одного года;
s(t) – остаточная (ликвидная) стоимость в году t;
Р – стоимость нового оборудования.
В качестве управлений выступают решения о замене и сохранении оборудования, принимаемые в начале каждого нового этапа. Обозначим через u1 – решение о сохранении оборудования, а через u2 – решение о замене оборудования. Тогда задача состоит в нахождении такой стратегии управления, определяемой решениями, принимаемыми в начале каждого этапа, при которой общий доход предприятия от эксплуатации оборудования является максимальной.
Таким образом, мы сформулировали исходную задачу в терминах задачи динамического программирования. Составим функциональное уравнение Р. Беллмана.
По условию задачи к началу k-го этапа (шага) может быть принято только одно из двух решений – сохранить или заменить оборудование. Поэтому установим зависимость между параметрами модели задачи на двух смежных этапах. Если сохранить оборудование, возраст которого t лет, то доход предприятия от его использования состоит из дохода r(t) на k-м этапе и дохода, полученного за (k – 1) оставшихся этапов при работе на оборудовании, возраст которого (t + 1) лет, т.е.
fk(t) = r(t) + fk–1(t + 1). (6.4)
В рассматриваемом процессе возраст оборудования t отсчитывается в прямом направлении, а этапы, на которые разбит процесс – в обратном.
Если на k-м этапе оборудование, возраст которого t лет, заменить новым, то доход после такой замены состоит из средства, полученного из разности между суммой ликвидной стоимости и дохода от эксплуатации нового оборудования [s(t) + r(0)] и стоимостью нового оборудования и плюс дохода, полученного за (k – 1) оставшихся этапов при работе на оборудовании, возраст которого (t + 1) = (0 + 1) лет
fk(t) = s(t) – p + r(0) + fk–1(1). (6.5)
Таким образом, если величина дохода, определенная из выражения (6.4) больше или равна величине дохода, определенной из выражения (6.5), то нужно работать на старом оборудовании, в противном случае оборудование следует заменить.
Объединив выражения (6.4) и (6.5) запишем основное функциональное уравнение
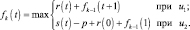 (6.6)
(6.6)
Здесь верхняя строка в правой части определяет доход, который может быть получен при работе на старом оборудовании, нижняя – при его замене. При этом предполагается, что переход к работе на новом оборудовании происходит за один этап.
Полагая в (6.6) k = 1, получим функциональное уравнение одноэтапного процесса для которого слагаемые fk–1(t + 1) и fk–1(1) не имеют смысла, так как этот этап соответствует завершающему году планирования работы предприятия. Поэтому исключая их из выражения (6.6) получим
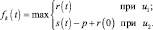 (6.7)
(6.7)
Пример 6.3 [42]. Условия задачи заданы в табл. 6.1. Пусть возраст оборудования к началу его эксплуатации составляет 1 год. Необходимо составит оптимальный производственный план работы предприятия за n = 6 лет и найти максимальную величину суммарного дохода предприятия за этот период с учетом возможной замены оборудования и определить год такой замены.
Таблица 6.1
|
t, лет |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
r(t), млн т. |
8 |
7 |
7 |
6 |
6 |
5 |
5 |
|
s(t), млн т. |
12 |
10 |
8 |
8 |
7 |
6 |
4 |
|
p, млн т. |
13 |
||||||
Решение. Поиск оптимальной стратегии предприятия, как было указано выше, начнем с первого этапа, где рассматривается последний шестой год планируемого периода.
Условная оптимизация
Шаг 1. Для первого этапа (k = 1), соответствующего завершающему периоду планирования работы предприятия, возможными сроками эксплуатации оборудования являются t = 1, 2, 3, 4, 5, 6. Эти значения примем как возможные состояния системы. Функциональное уравнение имеет вид (6.7):
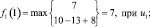
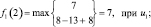
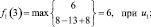
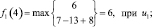
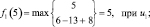
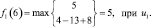
Шаг 2. Для второго этапа (k = 2) возможными сроками эксплуатации оборудования являются t = 1, 2, 3, 4, 5. Эти значения примем как возможные состояния системы. Функциональное уравнение, соответствующее формуле (6.6) для этого этапа имеет вид
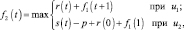
и подставляя возможные состояния системы получим:
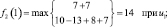
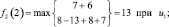
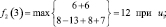
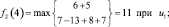
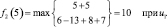
Шаг 3. Для третьего этапа (k = 3) возможными сроками (состояниями) эксплуатации оборудования являются t = 1, 2, 3, 4. Функциональное уравнение, соответствующее формуле (6.6) для этого этапа имеет вид
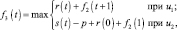
и подставляя возможные состояния системы получим:
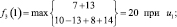
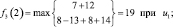
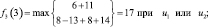
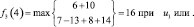
Шаг 4. Для четвертого этапа (k = 4) возможными сроками эксплуатации оборудования являются t = 1, 2, 3. Функциональное уравнение, соответствующее формуле (6.6) для этого этапа имеет вид
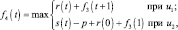
и подставляя возможные состояния системы получим:
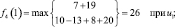
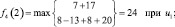
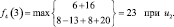
Шаг 5. Для пятого этапа (k = 5) возможными сроками эксплуатации оборудования являются t = 1, 2. Функциональное уравнение, соответствующее формуле (6.6) для этого этапа имеет вид
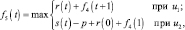
и подставляя возможные состояния системы получим:
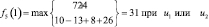 ;
;
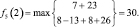
Шаг 6. Для пятого этапа (k = 6) возможным сроком эксплуатации оборудования является t = 1. Функциональное уравнение, соответствующее формуле (6.6) для этого этапа имеет вид
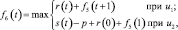
и подставляя возможное состояние системы получим:
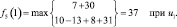
Таким образом, мы определили условно оптимальные доходы предприятия в зависимости от состояний t оборудования.
Результаты вычислений сведем в табл. 6.2. В таблице жирным курсивом выделено значение дохода, соответствующее управлению «замена оборудования».
Таблица 6.2
|
t k |
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
37 |
|||||
|
5 |
31 |
30 |
||||
|
4 |
26 |
24 |
23 |
|||
|
3 |
20 |
19 |
17 |
16 |
||
|
2 |
14 |
13 |
12 |
11 |
10 |
|
|
1 |
7 |
7 |
6 |
6 |
5 |
5 |
Безусловная оптимизация. Она начинается с начала планирования работы предприятия, которому соответствует этап k = 6. На этом этапе, как следует из предыдущих расчетов, с учетом начального условия t = 1 из табл. 6.1 имеем доход в объеме r(t=1) = 7 млн т., так как на этом этапе принято управление u1 (сохранении оборудования). Тогда к началу второго года (этап k = 5) возраст оборудования увеличится на единицу и станет равным t = 2 с годовым доходом r(t=2) = 7 при сохранении старого оборудования. В третьем году (этап k = 4) как следует (табл. 6.2) из условного максимума f4(3) принято управление u2 о замене оборудования и следовательно, годовой доход r(t=0) = 8. К этому доходу добавляется ликвидная стоимость s(t=3) и отнимается стоимость нового оборудования р. В четвертом году имеем параметры k = 3 и t = 1 и управление u1 с годовым доходом r(t=1) = 7. Пятый год характеризуется параметрами k = 2; t = 2 и управлением u1. Соответственно r(t=2) = 7. И наконец шестой год описывается параметрами k = 1; t = 3; r(t=3) = 6.
Таким образом, за 6 лет эксплуатации этого вида оборудования замену надо произвести один раз – в начале третьего года эксплуатации. При этом суммарный максимальный доход предприятия составит
f = r(t=1) + r(t=2) + r(t=0) + s(t=3) – p + r(t=1) + r(t=2) + r(t=3) = = 7 + 7 + 8 – 13 +8 + 7 + 7 + 6 = 37 млн т.
