
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.1. Модели операций. Задачи математического программирования
1. Задачи математического программирования.
2. Линейное программирование. Интерпретация задач линейного программирования.
3. Задача распределения ресурсов. Аксиомы линейности.
1. Задачи математического программирования
Основная задача математического программирования. Рассмотрим множество:
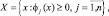 (4.1)
(4.1)
где ϕj(x) – заданные скалярные функций; x = (x1, ..., xk) – вектор входных параметров объекта, альтернативы.
Пусть скалярная функция f(x) определена на множестве Х. Задачу минимизации функции f(x) на множестве Х будем называть основной задачей математического программирования.
Форма записи задачи математического программирования.
Запись:
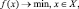 (4.2)
(4.2)
или, ей эквивалентный запись:
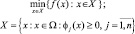
означает, что ставится задача:
1) либо найти оптимальную точку x* ∈ X:
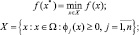
2) либо, если существует такая х*, то найти
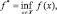
где inf f(x) – нижняя граница функции f(x).
3) либо: убедиться в том, что Х = ∅.
Если множества Х выпукло и выпукла функция f(x), то задачу (4.2) называют задачей выпуклого программирования.
Множество Х в задаче (4.2) называют допустимым множеством, точки этого множества – допустимыми точками; множество 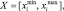
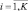 – исходным множеством альтернатив; неравенство ϕj(x) ≥ 0,
– исходным множеством альтернатив; неравенство ϕj(x) ≥ 0, 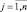 , определяющие допустимое множество – ограничениями. Точку
, определяющие допустимое множество – ограничениями. Точку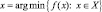 называют решением или оптимальной точкой. Точку х, в которой выполняется необходимые условия, локального минимума функции f(x) на множестве Х, будем называть стационарной.
называют решением или оптимальной точкой. Точку х, в которой выполняется необходимые условия, локального минимума функции f(x) на множестве Х, будем называть стационарной.
Задачи математического программирования должна содержать некую целевую функцию, оптимум которой следует определить, систему равенств и неравенств, описывающих условия-ограничения.
Общая задача математического программирования состоит в определении вектора х* с координатами 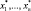 , которой является решением задачи:
, которой является решением задачи:
opt f(x),
при 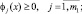
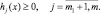
Общую задачу математического программирования разбивают на задачи, названия которых определяются видом оптимизируемой функции, функций, входящих в условия – ограничения, типом переменных и алгоритмом решения:
– линейного программирования f(x), ϕj(x), hj(x) – линейны;
– нелинейного программирования – хотя одна из функций f(x), ϕj(x), hj(x) нелинейные;
– квадратичного программирования – f(x), является квадратичной функцией, ограничения (ϕj(x), hj(x)) нелинейные;
– сепарабельного программирования f(x) – представляет собой сумму функций, различных для каждой переменной, условия – ограничения могут быть как линейными, так и нелинейными;
– целочисленного программирования функция f(x) – выпукла, ϕj(x), hj(x) – вогнутые, решения представляют собой целочисленные значения.
2. Линейное программирование. Интерпретация задач линейного программирования
Наиболее разработанными в математическом программировании являются задачи линейного программирования (ЛП) Модели ЛП занимают чрезвычайно важное место среди известных моделей экономических явлений и производственных процессов.
В общем случае задача линейного программирования сводится к следующему: требуется найти некоторую совокупность переменных, удовлетворяющих системе ограничений в форме равенств или неравенств и минимизирующую (максимизирующую) линейную функцию. Следовательно, формально имеем задачу:
Найти точку x = (x1, ..., xk), n-мерного пространство, которая удовлетворяют системе ограничений:
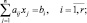 (4.3)
(4.3)
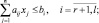 (4.4)
(4.4)
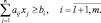 (4.5)
(4.5)
и минимизирует (максимизирует) линейную функцию:
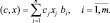 (4.6)
(4.6)
Это общая задача линейного программирования.
Множество точек х, удовлетворяющих (4.3)–(4.5), называется допустимым множеством (областью) и обычно обозначается буквой D. Любая точка допустимого множества называется допустимой точкой (допустимым решением, вектором, планом). Линейная функция, подлежащая минимизации или максимизации, называется целевой функцией. Допустимая точка, которая минимизирует (максимизирует) целевую функцию, называется решением задачи ЛП, оптимальным планом.
Очевидно, задача максимизации целевой функции (с, х) при каких-либо ограничениях эквивалентна задаче минимизации –(с, х). При этом
max(c, x) = –min[–(c, x)].
Естественным ответом на вопрос о том, как решать сформулированную задачу ЛП (4.3)–(4.6), кажется следующий метод простого перебора: найти произвольное решение х1 системы (4.3)–(4.5), вычислить (с, х1), затем найти другое решение х2, вычислить (с, х2) и т.д. и среди полученного спектра значений целевой функции (с, х), выбрать наименьшее. Значение х, реализующее минимум целевой функции, будет решением задачи ЛП. Но этот путь перебора оказывается труднореализуемым или даже нереализуемым в силу сложности поиска допустимых решений задачи ЛП. Допустимая область имеет, вообще говоря, бесконечное множество точек и может являться многогранным множеством. Это, в частности, означает, что если D принадлежат две какие-либо точки, то D принадлежат и все точки, соединяющего эти точки.
С геометрической точки зрения решением задачи ЛП является одна из вершин допустимого множества, тем самым решение сводится к перебору конечного числа вершин.
Для простоты рассуждений рассмотрим задачу ЛП в двумерном пространстве.
Пусть ограничения задачи имеют следующий вид:
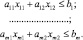 (4.7)
(4.7)
Требуется найти минимум целевой функции
(c, x) = c1x1 + c2.
Допустим, что система (4.7) совместно и соответствующее ей многогранное множество ограничено, т.е. является многоугольником. Очевидно, что каждое из неравенств (11.7) определяет полуплоскость соответственно с граничной прямой
ai1x1 + ai2x2 ai2x2 ≤ bi, i = 1, ..., m
и целевая функция принимает одно и то же значение f во всех точках прямой
c1x1 + c2x2 = f,
где f – некоторая константа.
При изменении (уменьшение или увеличение) получаем семейство параллельных прямых, называемых линиями уровня функции c1x1 + c2x2. Предположим, что многоугольник и линии уровня имеют вид, представленной на рис. 4.1. Нас интересуют те точки многоугольника D, которые принадлежат линии уровня с наименьшим значением f. Известно, что если перемещать прямую c1x1 + c2x2 = f в направлении ее нормали с, то значение f будет убывать.
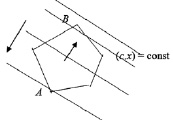
Рис. 4.1
Выберем достаточно большое f и будем перемещать прямую c1x1 + c2x2 = f в направлении –с. При этом линии уровня (с, х) = f вначале впервые коснется многоугольника, потом пересчет его и, наконец наступит момент, когда она коснется многоугольника в последний раз. Из рис. 4.1 следует, что прямая будет соприкасаться с многоугольником в точках А и В, причем в А значение целевой функции минимально.
Если же многоугольник не ограничен, то может быть два случая:
1) прямая, передвигаясь в направлении –с, все время пересекает многоугольник D; в этом случае линейная форма не ограничена на допустимой области и ее минимум равен –∞;
2) в результате передвижения вдоль направления –с прямая становится опорной к многоугольнику D.
Угловыми (крайними) точками выпуклого множества называются точки, не являющиеся выпуклой комбинацией двух различных точек этого множества. Угловые точки многогранника называются его вершинами.
Итак, геометрическая интерпретация подсказывает нам, что решением задачи ЛП может быть крайняя точка допустимого множества.
Теорема. Пусть допустимое множество D задачи линейного программирования (4.3)–(4.6) является многогранником. Тогда целевая функция (4.6) достигает своего минимума в вершине D. Если линейная форма принимает минимальное значение более чем в одной точке, то она достигает того же значения в любой точке, являющейся их выпуклой комбинацией.
Экономическая интерпретация задач линейного программирования
Задачу ЛП
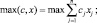
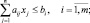 (4.8)
(4.8)
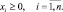
можно интерпретировать как задача производственного планирования. Оно состоит в определении такого набора х1, …, хn, интенсивностей технологических процессов, который удовлетворяют ограничениям по ресурсам, плановым заданиям по ресурсам, плановым заданиям и максимизирует суммарные доходы предприятия.
Двойственной задаче (4.8), т.е.:
min (u, b);
uA ≥ c; (4.9)
u ≥ 0
и переменным можно придать следующий смысл.
Пусть ui ≥ 0 – удельная оценка i-го ингредиента, измеренная в тех же единицах, в которых измеряется доход (убыток) каждой технологии. Тогда 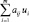 представляет собой суммарную оценку всех затрат предприятия, связанных с работой по j-й технологии с единичной интенсивностью. Ограничения же двойственной задачи
представляет собой суммарную оценку всех затрат предприятия, связанных с работой по j-й технологии с единичной интенсивностью. Ограничения же двойственной задачи
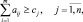
являются вполне естественными, так как предполагается, что учтены все затрачиваемые факторы, в том числе вложенный и производство труд, и, следовательно, результат производства (доход или убыток) не может превышать затрат.
Целевая функция двойственной задачи 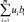 выражает суммарную
выражает суммарную
оценку всех ингредиентов. Тогда задача, двойственная к общей задаче производственного планирования, может быть интерпретирована как задача нахождения таких удельных оценок всех ингредиентов, участвующих в производстве, для которых суммарная оценка минимальна. При этом оценки должны быть такими, чтобы суммарная оценка каждой технологии при единичной интенсивности была не меньше соответствующего дохода (убытка).
3. Задача распределения ресурсов. Аксиомы линейности
Задача распределения ресурсов. На предприятии, выпускающем неоднородную продукцию, необходимо определить уровни производства для каждого продукта в течение заданного периода времени. Уровни производства имеют ряд ограничений:
– технологические;
– сырьевые;
– людские и т.д.,
заданных линейными соотношениями.
В рамках этих ограничений необходимо оптимизировать целевую функцию.
Целью можно считать получение максимальной прибыли (целей может быть больше чем одна, что чаще всего имеет место).
Допустим, фирма реализует 1–4 технологических процессов. Технологические процессы 1 и 2 ориентированы на выпуск продукции А, 3 и 4 ориентированы на выпуск продукта В.
Расходы каждого технологического процесса определяются трудозатратами (в человеко-неделях), недельным потреблением материала Y и Z.
Поскольку затраты на разных технологических процессах не одинаковые, прибыльность процессов окажется разной.
Далее необходимо принять допущения относительно технологии производства, которые обеспечат линейность модели. Назовем их аксиомами линейности.
1. Делимость. Для каждого технологического процесса (Т.П.) суммарное потребление каждого из потребляемых ресурсов и прибыль пропорциональны объему выпускаемой продукции.
а) Т.е. все показатели Т.П. могут быть увеличены или уменьшены при сохранении их взаимной пропорциональности.
Для выпуска 10 единиц продукции x1 необходимо 10 человеко-недель, 70 единиц материала Y, 30 единиц материала Z. Доход составит 40 единиц.
б) Все производственно-экономические показатели могут принимать как целочисленные, так и вещественные значения.
При составлении производственного плана на неделю примем следующие производственно-экономические показатели и ограничения:
2. Аддитивность. Если значения каждой из управляющих переменных xj определенно, то полное количество каждого из потребленных ресурсов равняется сумме одноименных ресурсов, затраченных при реализации всех Т.П., а полная прибыль равна сумме прибылей всех Т.П.
Принятие аксиом делимости и аддитивности эквивалентно утверждению о представлении математической модели в виде линейных соотношений. А именно: доходы строго пропорциональны затраченным ресурсам.
В реальных ситуациях такое утверждение можно принимать лишь приближенно.
В рассматриваемом примере будем считать все три неравенства, которые можно составить, задаются линейными соотношениями:
4x1 + 5x2 + 9x3 + 11х4 ≡ max; (4.10)
1x1 + 1x2 + 1x3 + 1x4 ≤ 15 (колич. человеко-недель);
7x1 + 5x2 + 3x3 + 2x4 ≤ 120 (ед. материала Y); (4.12)
3x1 + 5x2 + 10x3 + 15x4 ≤ 100 (ед. материала Z).
Уравнение (4.11) определяет суммарную прибыль производственно-технологического процесса из табл. 4.1.
Таблица 4.1
На 1 ед.
продукции А
На 1 ед.
продукции В
Имеется в наличии (всего)
Т.п. 1
Т.п. 2
Т.п. 3
Т.п. 4
Количество человеко-недель
1
1
1
1
≤ 15
Количество материала Y (кг)
7
5
3
2
≤ 120
Количество материала Z (в ящиках)
3
5
10
15
≤ 100
Доход с 1 ед. продукции ($)
4
5
9
11
max
Объем выпускаемой продукции
x1
x2
x3
x4
Уравнения (4.12) определяют суммарные трудозатраты, потребление материалов Y и Z. Следует принять дополнительные ограничения:
х1 ≥ 0; х2 ≥ 0; х3 ≥ 0; х4 ≥ 0. (4.13)
Каждая из управляемых переменных должна быть неотрицательной.
Задача сводится к определению управляемых переменных х1, х2, х3, х4, удовлетворяющих соотношениям (4.11), (4.12), (4.13). Для начала в ограничениях (4.12) примем предельные значения. Тогда формальная запись задачи примет вид:
1x2 + 1x3 + 1x4 = 15 (колич. человеко-недель);
7x1 + 5x2 + 3x3 + 2x4 = 120 (ед. материала Y); (4.12′)
3x1 + 5x2 + 10x3 + 15x4 = 100 (ед. материала Z);
xj ≥ 0 (j = 1, 2, …, n). (4.13′)
Определим максимальные значения переменных, входящих в целевую функцию, с наибольшими коэффициентами. Считаем, что они наиболее существенно влияют на значение целевой функции (ц.ф.).
Из (4.12′) при условии х1 = х2 = х3 = 0; х4 = 15; х4 = 60; х4 = 66.
Пробное значение х4 = 60, ц.ф. = 11·60 = 660
при условии х1 = х2 = х4 = 0; х3 = 15; х3 = 40; х3 = 10.
Пробное значение х3 = 40; ц.ф. = 9·40 = 360.
при условии х1 = х3 = х4 = 0; х2 = 15; х2 = 24; х2 = 20.
Пробное значение х2 = 24; ц.ф. = 5·24 = 120.
при условии х2 = х3 = х4 = 0; х1 = 15; х1 = 17,1; х1 = 33,3.
Пробное значение х1 = 33,3; ц.ф. = 4·33,3 = 133,2.
Из предварительного анализа видно, что на целевую функцию наиболее существенно влияют х4 и х3, так как при пробных значениях они дают наибольшее значение целевой функции. Подбирая различные комбинации xj можно найти такую, при которой значение целевой функции стремится к максимальному.
Такую комбинацию можно считать оптимальной. Однако такой метод весьма трудоемкий и длительный.
Оптимальное соотношение значений управляющих переменных можно найти методом исключения переменных в системе (4.12′) или методом Гаусса.
Допустим, что оптимальное решение можно найти комбинацией х3 и х4 при нулевых значениях х1 и х2. Из (4.12′):
х3 + х4 = 15 – х1 – х2; (4.14)
3х3 + 2х4 = 120 – 7х1 – 5х2; (4.15)
10х3 + 15х4 = 100 – 3х1 – 5х2. (4.16)
Из (4.16) исключим х3. Для этого (4.14) умножим на 10 и вычтем из (4.16)
5х4 = –50 + 7х1 + 5х2. (4.17)
Пронормируем коэффициент при х4 в (4.17)
х4 = –10 + 7/5х1 + х2. (4.18)
Исключим х4 из (4.15). Для этого (4.18) умножим на 2 и вычтем из (4.15)
3х3 = 140 – 49/5х1 – 7х2. (4.19)
Пронормируем коэффициент при х3 в (4.9)
х3 = 140/3 – 49/5х1 – 7/3х2. (4.20)
Из (4.20) при х1 = х2 = 0; х3 = 140/3 = 46,6 что превышает пробное значение х3 = 40. Из (4.18) х4 = –10, что противоречит ограничениям. Следовательно, необходимо выбрать следующую пару управляющих переменных и решить систему относительно их.
Для управляющих переменных х1, х4 имеем:
х1 + х4 = 15 – х2 – х3;
7х1 + 2х4 = 120 – 5х2 – 3х3;
3х1 + 15х4 = 100 – 5х2 – 10х3.
Приводим к системе методом Гаусса
х1 + х4 = 15 – х2 – х3;
х1 = 18 – 3/5х2 – 1/5х3;
х4 = 55/12 – 1/6х2 – 7/12х3.
Из допущения х2 = х3 = 0 следует, что х1 = 18; х4 = 4,6; целевая функция = 4·18 + 11·4,6 = 122,6.
Улучшением решения можно считать определение значений управляющих переменных, при которых значения целевой функции будет расти.
Заключение. В данном подразделе рассмотрена изучена основная задача математического программирования, рассмотрены виды задач математического программирования, в т.ч. задача линейное программирование. Дана интерпретация задач линейного программирования. Изучен и приведен пример к задаче распределения ресурсов. Рассмотрены аксиомы линейности.
Контрольные вопросы
1. Основная задача математического программирования.
2. Виды задач математического программирования.
3. Задача линейное программирование.
4. Интерпретация задач линейного программирования.
5. Задача распределения ресурсов.
6. Аксиомы линейности.
