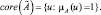Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
ГЛОССАРИЙ
А
Абстрактные системы – это умозрительное представление образов или моделей материальных систем.
Абстрагирование – установление общих свойств и сторон объекта (или объектов), замещение объекта или системы ее моделью.
Абстракция – описание, представление объекта (явления), получаемое с помощью метода абстрагирования;
Адаптивность – стремление системы к состоянию устойчивого равновесия, которое предполагает адаптацию параметров системы к изменяющимся параметрам внешней среды.
Аксиома инвариантности относительно линейного преобразования – если платежные матрицы двух игр с одинаковым числом ходов для каждого игрока инвариантны относительно линейного преобразования, то и соответствующие арбитражные решения инвариантны относительно линейного преобразования с теми же коэффициентами инвариантности.
Аксиома независимости несвязанных альтернатив – если к игре добавить новые ходы игроков с добавлением новых элементов платежных матриц таким образом, что точка status quo не меняется, то либо арбитражное решение также не меняется, либо оно совпадает с одной из добавленных сделок.
Аксиома оптимальности по Парето – арбитражное решение должно быть элементом переговорного множества.
Аксиома симметрии в теории игр – если игроки находятся в одинаковой ситуации, то и арбитражное решение должно быть одинаковым.
Аксиоматические методы – определяется ряд аксиомы, которым должна удовлетворять зависимость общей полезности от оценок по локальным критериям.
Алгоритм двойственного симплекс-метода – алгоритм последовательного улучшения плана, применимого к задаче минимизации целевой функции, при этом допустимая область определяется следующим образом: компоненты произведения матрицы ограничений и вектора переменных должны быть больше либо равны соответствующих компонент вектора ограничений. Условие неотрицательности переменных не накладывается.
Алгоритм метода ветвей и границ – алгоритм одного из комбинаторных методов дискретного программирования, при котором гиперплоскость, определяемая целевой функцией задачи, вдавливается внутрь многогранника планов соответствующей задачи линейного программирования до встречи с ближайшей целочисленной точкой этого многогранника.
Алгоритм метода Гомори – один из алгоритмов нахождения решения задачи целочисленного программирования.
Алгоритм симплекс-метода – алгоритм последовательного улучшения плана, позволяющий осуществлять переход от одного допустимого базисного решения к другому таким образом, что значение целевой функции непрерывно возрастает и за конечное число шагов находится оптимальное решение.
Алгоритм улучшения плана транспортной задачи – алгоритм перехода к новому опорному плану транспортной задачи, дающему меньшее значение функции потерь, до обнаружения оптимального плана.
Анализ – разъединение системы на подсистемы с целью выявления их взаимосвязей.
Антагонистические игры – игры, в которых интересы игроков строго противоположны, т.е. выигрыш одного игрока – проигрыш другого.
Арбитраж – нахождение совместной стратегии с помощью незаинтересованного лица.
Булевское программирование – раздел математического программирования, занимающийся разработкой методов решения специфических задач целочисленного программирования, когда переменные могут принимать значения 1 или 0.
База знаний – ядро интеллектуальных систем, совокупность знаний предметной области, записанная на машинный носитель в форме, понятной эксперту и пользователю (обычно на некотором языке, приближенном к естественному). Параллельно такому «человеческому» представлению существует база знаний во внутреннем «машинном» представлении.
Визуализация – получение информации с помощью наглядного или визуального представления состояний актуализированной системы.
Вектор коэффициентов – вектор, компонентами которого являются коэффициенты целевой функции задачи линейного программирования.
Вектор ограничений – вектор, компонентами которого являются ограничения выражений, определяющих допустимую область задачи линейного программирования.
Вершина выпуклого многогранника – это любая точка выпуклого многогранника, которая не является внутренней никакого отрезка целиком принадлежащего этому многограннику.
Выбор решений при неопределенности – игры, где одним из определяющих факторов является внешняя среда или природа, которая может находится в одном из состояний, которые неизвестны лицу, принимающему решение.
Выпуклая комбинация точек – точка, компоненты которой представлены суммой произведений неотрицательных коэффициентов не больших единицы и соответствующих компонент данных точек, при этом сумма всех коэффициентов равна единице.
Выпуклое множество – множество, которое вместе с двумя принадлежащими ему точками обязательно содержит отрезок, соединяющий эти точки.
Выпуклое программирование – раздел математического программирования, где целевая функция и функции, определяющие допустимую область, являются выпуклыми.
Вырожденный опорный план – опорный план, число ненулевых компонент которого меньше числа ограничений.
Генетический алгоритм – это простая модель эволюции в природе, реализованная в виде компьютерной программы. В нем используются как аналог механизма генетического наследования, так и аналог естественного отбора. При этом сохраняется биологическая терминология в упрощенном виде.
Геометрическая интерпретация задачи линейного программирования – интерпретация зависимостей, имеющих место в задаче линейного программирования в виде геометрических фигур (точек, прямых, полуплоскостей, многоугольников) в декартовой системе координат.
Геометрическое программирование – раздел математического программирования, занимающийся задачами наиболее плотного расположения объектов в заданной двумерной или трехмерной области.
Данные – синтаксические сигналы, образы, актуализируемые с помощью некоторого источника данных. Они рассматриваются безотносительно к семантическому их смыслу.
Двойственные задачи линейного программирования – задачи линейного программирования, которые могут быть составлены из исходных задач линейного программирования согласно соответствующим правилам.
Дедукция – получение знания о подсистемах по знаниям о системе; дедуктивное мышление: определение проблемы и затем поиск ситуации, ее разрешающей.
Декомпозиция – разъединение системы на подсистемы с сохранением их взаимосвязей с окружением.
Дельта-метод – один из методов проверки опорного плана транспортной задачи на оптимальность.
Дефаззификация (defuzzification) – процедура преобразования нечеткого множества в четкое число.
Динамическое программирование – вычислительный метод решения экстремальных задач определенной структуры, представляющий собой направленный последовательный перебор вариантов, который обязательно приводит к глобальному максимуму.
Дискретное программирование – раздел математического программирования, в котором на экстремальные задачи налагается условие дискретности переменных при конечной области допустимых значений.
Дихотомическая шкала – позволяет отметить, относится ли данный объект к интересующей нас группе или нет.
Допустимая область задачи линейного программирования – множество опорных планов задачи линейного программирования.
Задача коммивояжера – коммивояжер должен посетить один, и только один, раз каждый из n городов и вернуться в исходный пункт. Его маршрут должен минимизировать суммарную длину пройденного пути.
Задача линейного программирования – характеризуется тем, что целевая функция является линейной функцией переменных, а область допустимых значений определяется системой линейных равенств или неравенств.
Задача математического программирования – в общей постановке задачи этого раздела выглядят следующим образом. Имеются какие-то переменные x = (x1, x2, ..., xn) и функция этих переменных f(x) = f(x1, x2, ..., xn), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G.
Задача нечеткого математического программирования – обобщенный класс задач математического программирования, который в частных случаях, когда функции принадлежности нечетких переменных преобразуются в обычным задачам математического программирования. Здесь либо целевые функций, либо ограничений, либо все они характеризуются нечеткостью.
Задача о диете – возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям.
Задача о назначении – имеем n исполнителей, которые могут выполнять n различных работ. Известна полезность cij, связанная с выполнением i-м исполнителем j-й работы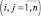 
. Необходимо назначить исполнителей на работы так, чтобы добиться максимальной полезности, при условии, что каждый исполнитель может быть назначен только на одну работу и за каждой работой должен быть закреплен только один исполнитель.
Задачи принятия решений при риске – возникают в тех случаях, когда с каждым принимаемым решением xI ∈ Ω связано множество исходов из m возможных результатов S1, …, Sn с известными вероятностями P(SJ | xi), j = 1, n, i = 1, m, т.е. в этих задачах нет однозначной связи между альтернативами и исходом.
Задача о рюкзаке –контейнер оборудован m отсеками вместимостью bi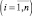 
для перевозки n видов продукции Пi 
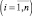. Виды продукции характеризуются свойством неделимости, т.е. их можно брать в количестве 0, 1, 2, ... единиц. Пусть αij – расход i-го отсека для перевозки единицы j-й продукции. Обозначим через cj полезность единицы j-й продукции. Требуется найти план x = (x1, x2, ..., xn) перевозки, при котором максимизируется общая полезность рейса.
Задача о составлении плана производства – возникает при необходимости максимизации дохода от реализации продукции, производимой некоторой организацией, при этом производство ограничено имеющимися сырьевыми ресурсами.
Задачи принятия решений – возникает при выборе или принятия решений из нескольких возможных альтернатив решений оптимального по заданным критериям решения.
Задачи приятия решений при риске – необходимо принимать решения в условиях вероятности.
Задачи принятия решений в нечеткой среде – характеризуются тем, что исходные данные (альтернативы, критерий), необходимые для принятия решении описываются нечетко.
Задачи управления – имеются четыре основных задачи управления: стабилизация; программное управление; слежение; оптимальное управление.
Замкнутая система управления – позволяет быстро реагировать на нежелательные отклонения в поведении объекта, с целью устранить отклонения.
Знания – информация, обеспечивающая достижение некоторой цели и структуры.
Е
Естественные системы – представляют собой совокупность объектов природы и подразделяются на астрокосмические и планетарные, физические и химические.
Игра n лиц с постоянной суммой – игры, в которых принимает участие n игроков, существует n множеств стратегий и n действительных платежных функций от n переменных, каждая из которых является элементом соответствующего множества стратегий. Каждый игрок знает всю структуру игры и в своем поведении неизменно руководствуется желанием получить максимальный средний выигрыш.
Игра двух лиц с ненулевой суммой – игры, в которых сумма выирышей двух игроков после каждой партии не равна нулю.
Игра двух лиц с нулевой суммой – игры, в которых интересы двух игроков строго противоположны, т.е. выигрыш одного есть проигрыш другого.
Игра против природы – игры, где одним из определяющих факторов является внешняя среда или природа, которая может находится в одном из состояний, которые неизвестны лицу, принимающему решение.
Игра с нулевой суммой – игры, в которых сумма выигрыша игроков после каждой партии составляет ноль.
Идеализация – получение знаний о системе или о ее подсистемах путем мысленного конструирования, представления в мышлении систем и/или подсистем, не существующих в действительности.
Иерархичность – каждый компонент системы может рассматриваться как система; сама система также может рассматриваться как элемент некоторой надсистемы (суперсистемы).
Инженер по знаниям – специалист по искусственному интеллекту, выступающий в роли промежуточного буфера между экспертом и базой знаний. Синонимы: когнитолог, инженер-интерпретатор, аналитик.
Интегративность – наличие в системе системообразующих, системосохраняющих факторов.
Интеллектуальные системы – системы, основанные на знаниях (Knowledge Based System) – поддерживают задачи принятия решения в сложных системах, где необходимо использование знаний в достаточно широком диапазоне, особенно в плохо формализуемых и плохо структурируемых системах и при нечетких критериях принятия решения.
Интеллектуальный редактор БЗ – программа, представляющая инженеру по знаниям возможность создавать БЗ в диалоговом режиме. Включает в себя систему вложенных меню, шаблонов языка представления знаний, подсказок («help» – режим) и других сервисных средств, облегчающих работу с базой.
Индукция – получение знания о системе по знаниям о подсистемах; индуктивное мышление: распознавание эффективных решений, ситуаций и затем проблем, которые оно может разрешать.
Информационные процессы – процессы сбора, хранения, обработки и передачи данных с целью управления производственным процессом и соответствующими структурными подразделениями.
Информационная система – система, в которой ее элементы, цель, ресурсы, структура (организация) рассматриваются, в основном, на информационном уровне (хотя, естественно, имеются и другие уровни рассмотрения, например, энергетический уровень).
Информационная система управления – система, предназначенная для управления, – как другой системой, так и внутри системы (т.е. в качестве управляющей подсистемы).
Исследование операций – наука, занимающаяся разработкой и практическим применением методов наиболее оптимального управления организационными системами.
Искусственные системы – это совокупность социально-экономических или технических объектов.
Каноническая форма задачи линейного программирования – форма задачи линейного программирования, в которой целевая функция требует нахождения минимума, переменные неотрицательны, а компоненты произведения матрицы ограничений и вектора переменных равны соответствующим компонентам вектора ограничений.
Классификация обслуживающих систем по времени пребывания требований в системе до начала обслуживания – системы с неограниченным временем ожидания; системы с отказами (вновь поступившее требование, застав все приборы занятыми, покидает систему); системы смешанного типа (поступившее требование становится в очередь, но, в отличие от (1), оно в очереди может находиться ограниченное время, после чего, не дождавшись обслуживания, покидает систему.
Композиция – соединение подсистем в систему с сохранением их взаимосвязей с окружением.
Компонент – есть либо неделимая часть, либо объект, состоящий из частей и называемый подсистемой.
Коммуникативность – существование сложной системы коммуникаций со средой в виде иерархии.
Концептуальная модель – это абстрактная модель, выявляющая причинно-следственные связи, присущие исследуемому объекту и существенные в рамках определённого исследования. Основное назначение концептуальной модели – выявление набора причинно-следственных связей, учёт которых необходим для получения требуемых результатов.
Классификация задач исследования операций – задачи можно разделить на три уровня: Детерминированный уровень; Стохастический уровень; Неопределенный уровень.
Классификация игр ненулевой суммой – игры с ненулевой суммой делятся на кооперативные и некооперативные.
Критерий минимаксного сожаления – пусть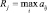 
, то есть Rj это максимум того, что может получить игрок при j-м состоянии Природы.
Перейдём от величин aij к величинам rij = Rj – aij, которые можно трактовать как «сожаление», то есть недополученная выгода от того, что при j-м состоянии Природы игрок сделал неправильный ход. Тогда
в качестве критерия для выбора хода предлагается следующий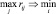 
, то есть минимизация максимального «сожаления».
Критерий оптимизма-пессимизма Гурвица – пусть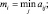 
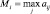, то есть mi и Mi есть минимум и максимум того, что может получить игрок, выбирая ход номер i. Свяжем с каждым ходом величину 
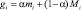и будем выбирать свой ход из условия 
.
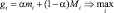Коэффициент α носит название показателя пессимизма игрока. При α = 1 мы имеем крайне пессимистичного человека, и этот критерий переходит в критерий максимина. При α = 0 перед нами убеждённый оптимист.
Линейное программирование – часть математического программирования, задачами которой является нахождение экстремума линейной целевой функции на допустимом множестве значений аргументов.
Лингвистическая переменная (linguistic variable) – переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка.
Максиминная стратегия – стратегия игрока, при которой он стремится сделать минимальный выигрыш максимальным, т.е. получить наилучшую выгоду в наихудших условиях.
Максиминный критерий – критерий, согласно которому происходит стремление получения максимального выигрыша в наихудшей ситуации.
Математическая модель – абстрактная модель, представленная на языке математических отношений. Она имеет форму функциональных зависимостей между параметрами, учитываемыми соответствующей концептуальной моделью. Эти зависимости конкретизируют причинно-следственные связи, выявленные в концептуальной модели, и характеризуют их количественно.
Математическое программирование – раздел современной математики, задачами которого является нахождение экстремума функции при условии принадлежности переменных определенному множеству.
Матрица коэффициентов – матрица, элементами которой являются коэффициенты системы линейных равенств или неравенств определенного типа.
Матричная форма задачи линейного программирования – форма задачи линейного программирования, когда все элементы задачи представлены в матричных и векторных обозначениях.
Матричные игры – игры, математические модели которых можно представить в виде матриц.
Метод ветвей и границ – один из комбинаторных методов дискретного программирования, при котором гиперплоскость, определяемая целевой функцией задачи, вдавливается внутрь многогранника планов соответствующей задачи линейного программирования до встречи с ближайшей целочисленной точкой этого многогранника.
Метод Гомори – один из методов отсечения, с помощью которого решаются задачи целочисленного программирования.
Метод искусственного базиса – один из методов, упрощающий определение исходного опорного плана задачи линейного программирования и симплекс-таблицы.
Метод минимального элемента – один из группы методов определения первоначального опорного плана транспортной задачи.
Метод «мозговой атаки» – преследуют основную цель – поиск новых идей, их широкое обсуждение и конструктивную критику. Основная гипотеза заключается в предположении, что среди большого числа идей имеются по меньшей мере несколько хороших.
Метод потенциалов – один из методов проверки опорного плана транспортной задачи на оптимальность.
Метод северо-западного угла – один из группы методов определения первоначального опорного плана транспортной задачи.
Методы отсечений – методы решения задач дискретного программирования, для которых характерна регуляризация задачи, состоящая в погружении исходной области допустимых решений в объемлющую ее выпуклую область, т.е. во временном отбрасывании условий дискретности, после чего к получившейся регулярной задачи применяются стандартные методы.
Методы компенсации – основаны на идее компенсации оценки одной альтернативы оценками другой, чтобы найти какие альтернативы лучше.
Метод порогов сравнимости – задается правило сравнения двух альтернатив, при котором одна альтернатива считается лучше другой
Метод «Дельфи» – является итеративной процедурой для проведения мозговой атаки, которая способствовала бы снижению влияния психологических факторов при повторении заседаний и повышения объективности результатов.
Метод «дерева целей» – термин «дерево» предполагает использование иерархической структуры, полученной путем разделения общей цели на подцели. Метод ориентирован на получение относительно устойчивой структуры целей проблем, направлений.
Методы экспертных оценок – основа этих методов – различные формы экспертного опроса с последующим оцениванием и выбором наиболее предпочтительного варианта.
Методология системного анализа – представляет совокупность принципов, подходов, концепций и конкретных методов, а также методик.
Метод – это прием или способ действия.
Методика – это совокупность методов, приемов проведения какой-либо работы.
Минимаксная стратегия – стратегия игрока, при которой он стремится сделать максимальный проигрыш минимальным.
Множество Парето – множество точек из R, которые не подчинены никаким другим точкам и для которых выполняется условие v ≥ v*, w ≥ w*.
Множество α-уровня – четкое подмножество универсального множества U, элементы которого имеют степени принадлежности большие или равные α: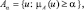 
α ∈ [0, 1].
Морфологические методы – основная идея морфологического подхода – систематически находить все возможные варианты решения проблемы путем комбинирования выделенных элементов или их признаков.
Нейронная сеть – способ моделирования в технических системах принципов организации и механизмов функционирования головного мозга человека.
Нейро-нечеткие сети – используют нечеткий логический вывод на основе системы нечетких правил, которая описывает опыт экспертов конкретной предметной области, представленный на качественном уровне.
Неструктурированная (неформализованная) задача – задача, в которой невозможно выделить элементы и установить между ними связи.
Нечеткое математическое программирование – математическое программирование, где присутствуют элементы нечеткости.
Нечеткое множество (fuzzy set) – 
на универсальном множестве U называется совокупность пар (μА(u), u), где μА(u) – степень принадлежности элемента u ∈ U к нечеткому множеству 
.
Нечеткий логический вывод (fuzzy logic inference) – аппроксимация зависимости y = f(x1, x2, …, xn) с помощью нечеткой базы знаний и операций над нечеткими множествами.
Носителем нечеткого множества – четкое подмножество универсального множества U, элементы которого имеют ненулевые степени принадлежности: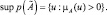 
Обслуживающие системы – системы массового обслуживания, характеризующиеся входящим потоком требований, приборами обслуживания, Очередью требований, выходящим потоком требований.
Оптимальный план ЗЛП – решение задачи линейного программирования, т.е. такой план, который входит в допустимую область и доставляет экстремум целевой функции.
Орган управления – это система, на вход которой поступают сигналы о состоянии управляемого объекта и среды, а на выходе – сигнал о необходимом в данной ситуации управлении.
Основная теорема линейного программирования – если целевая функция принимает максимальное значение в некоторой точке допустимой области, то она принимает это же значение в крайней точке допустимой области. Если целевая функция принимает максимальное значение более, чем в одной крайней точке, то она принимает это же значение в любой их выпуклой комбинации.
Открытая транспортная задача – несбалансированная транспортная задача.
Партия игры – совокупность действий игроков, определенная правилами игры и состоящая из ходов, после которых игрокам выплачиваются выигрыши.
Первая стандартная форма ЗЛП – форма задачи линейного программирования, в которой целевая функция требует нахождения максимума, переменные неотрицательны, а компоненты произведения матрицы ограничений и вектора переменных должны быть меньше либо равны соответствующих компонент вектора ограничений.
Переговорное множество – множество точек из R, которые не подчинены никаким другим точкам и для которых выполняется условие v ≥ v*, w ≥ w*.
План – набор чисел, удовлетворяющий ограничениям задачи линейного программирования.
Платежная матрица игры – матрица размерности m на n, i = 1, ..., n j = 1, ..., m (i, j)-й элемент которой значение выигрыша (пригрыша) игроков в случае i-го хода первого игрока и j-го хода второго игрока.
Поведение системы – если система способна переходить из одного состояния в другое (например, с1 → с2 → с3, то говорят, что она обладает поведением.
Подсистема – часть системы с некоторыми связями и отношениями.
Подcucmeмa объяснений – программа, позволяющая пользователю получить ответы на вопросы: «Как была получена та или иная рекомендация?» и «Почему система приняла такое решение?» Ответ на вопрос «как» – это трассировка всего процесса получения решения с указанием использованных фрагментов БЗ, т.е. всех шагов цепи умозаключений. Ответ на вопрос «почему» – ссылка на умозаключение, непосредственно предшествовавшее полученному решению, т.е. отход на один шаг назад.
Подход – это совокупность приемов, способов воздействия на кого-нибудь, в изучении чего-нибудь, ведении дела и т.д.
Позиционные игры – описание игры как последовательности ходов.
Потенциалы – переменные, соответствующие переменным двойственной задачи для данной транспортной задачи.
Принятие решения – заключается в оценке возможных вариантов решений (альтернатив) и выбор наилучшего из них по заданным критериям.
Предмет исследования операций – системы организационного управления, которые состоят из большого числа взаимодействующих подразделений, не всегда согласующихся между собой.
Предмет теории игр – принятие решений в условиях неопределенности, в условиях столкновения, конфликтных ситуациях, когда принимающий решение субъект (игрок), располагает информацией лишь о множестве возможных ситуаций, в одной из которых он в действительности находится, о множестве решений, которые он может принять, и о количественной мере того выигрыша, который он мог бы получить, выбрав в данной ситуации данную стратегию.
Предпосылки в играх – это вектора, компонентами которых является среднее значение дохода соответствующих игроков, которые объединились в коалицию, при этом доходы должны быть не меньше доходов, получаемых игроками вне коалиции, а весь доход коалиции должен быть распределен между игроками.
Признак вершины допустимой области – если система из k ненулевых векторов-столбцов, образованных соответствующими столбцами матрицы ограничений является линейно независимой и ненулевые координаты точки X, удовлетворяют ограничениям, то эта точка является вершиной допустимой области.
Принцип недостаточного основания – заключается в том, что все состояния природы считаются равновероятными.
Принцип новых задач – он состоит в том, что не следует просто перекладывать на автоматизированную систему традиционные приемы управления, а нужно их перестраивать в соответствии с возможностями и особенностями используемых методов и техники.
Принцип системного подхода – это означает, что цели и критерии функционирования объекта и системы информационного обеспечения должны рассматриваться совместно и для них должна быть проведена совместная структуризация, отражающая весь комплекс вопросов.
Принцип непрерывного развития системы – система должна быть способной реагировать на изменение экономических и других условий как на макроуровне, так и на уровне отдельных предприятий.
Принцип единой информационной базы – он заключается в том, что информация в системе накапливается и обновляется не отдельными частями, относящимися к отдельным задачам, а в виде единого целого, обеспечивающего дублирование информации и возможность разночтений.
Рабочий проект – это техническая документация, утвержденная в установленном порядке, содержащая уточненные данные и детализированные общесистемные проектные решения, программы и инструкции по решению задач, а также уточненную оценку экономической эффективности АСУ и уточненный перечень мероприятий по подготовке объекта к внедрению.
Равновесие системы – понятие равновесие определяют как способность системы в отсутствии внешних возмущающих воздействий (или при постоянных воздействиях) сохранять свое поведение сколь угодно долго.
Разомкнутая система управления – учитывает причины (возмущения среды), которые вызывают то или иное поведение объекта.
Решатель – программа, моделирующая ход рассуждений эксперта на основании знаний, имеющихся в базах знаний. Синонимы: дедуктивная машина, блок логического вывода.
Решение задачи линейного программирования – это план, доставляющий экстремальное значение целевой функции.
Решение игры – уравновешенная пара.
Сбалансированная транспортная задача – транспортная задача, в которой выполняется условие баланса.
Сговор в игре – совместные действия игроков с целью получения максимального выигрыша.
Седловой точка – действительной функции f(x), определённой для всех x ∈ A, y ∈ B, называется точка (x0, y0), где x0 ∈ A, y0 ∈ B, если выполнены следующие условия:
1. ∀x ∈ A, f(x, y0) ≤ f(x0, y0);
2. ∀y ∈ B, f(x0, y0) ≤ f(x0, y).
Симплекс метод – последовательное улучшение плана задачи линейного программирования, позволяющее осуществлять переход от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают и за конечное число шагов находится оптимальное решение.
Система – совокупность элементов, находящихся в определенных отношениях друг с другом и со средой.
Система поддержки принятия решений (Decision Support System) – система для анализа (моделирования) реальной формализуемой ситуации, в которой менеджер должен принять некоторое решение, возможно, просчитав различные варианты потенциального поведения системы (варьируя ее параметры); такие системы используются как в краткосрочном, так и в долгосрочном управлении тактического или стратегического характера в автоматизированном режиме.
Системный анализ – совокупность методов и средств выработки, принятия и обоснования оптимального решения из многих возможных альтернатив.
Системный подход – является теоретической и методологической основой системного анализа. Это подход к исследованию объекта как к системе, в которой выделены элементы, внутренние и внешние связи, наиболее существенным образом влияющие на исследуемые результаты его функционирования, и цели каждого из элементов, исходя из общего предназначения объекта. Он ориентирует на раскрытие целостности объекта и обеспечивающих его механизмов, на выявление многообразных типов связей сложного объекта и сведение их в единую теоретическую картину.
Синергичность – свойство системы – максимальный эффект деятельности системы достигается только в случае максимальной эффективности совместного функционирования её элементов для достижения общей цели.
Сообщения – полученные системой от внешнего мира в процессе адаптивного управления, приспособления (теория управления, кибернетика).
Состояние системы – понятием состояние обычно характеризуют мгновенную фотографию, «срез» системы, остановку в ее развитии.
Структурный подход – при структурном подходе выявляются состав выделенных элементов системы S и связи между ними. Совокупность элементов и связей между ними позволяет судить о структуре системы.
Т
Техническое задание – это документ, утвержденный в установленном порядке, определяющий цели, требования и основные исходные данные, необходимые для разработки АСУ системы управления, и содержащий предварительную оценку экономической эффективности системы.
Технический проект – это техническая документация, утвержденная в установленном порядке, содержащая общесистемные проектные решения, алгоритм решения задач, а также оценку экономической эффективности АСУ и перечень мероприятий по подготовке объекта к внедрению.
Теория систем – междисциплинарная область науки, рассматривающая поведение и взаимодействие различных систем в природе, обществе и науке. Основной целью теории систем является обнаружение основных принципов функционирования систем, необходимых для описания любой группы взаимодействующих объектов, во всех областях исследований.
У
Управление – это совокупность действий, направленных на обеспечение протекания процесса с достижением требуемых результатов.
Устойчивость системы – под устойчивостью понимают способность системы возвращаться в состояние равновесие после того, как она была из этого состояния выведена под влиянием внешних возмущающих воздействий.
Ш
Шкала абсолютная – результатом измерения в которой является число, выражающее количество элементов в множестве.
Шкала интервалов – можно менять как начало отсчёта, так и единицы измерения.
Шкала наименований (номинальная) – числа используются исключительно с целью обозначения объектов.
Шкала отношений – начало отсчёта неизменно, а единицы измерения можно изменять (масштабировать).
Шкала порядков (ранговые шкалы) – при измерении в которой мы получаем информацию лишь о том, в каком порядке объекты следуют друг за другом по какому-то свойству.
Ф
Формализация – получение знаний о системе с помощью знаков или же формул, т.е. языков искусственного происхождения, например, языка математики (или математическое, формальное описание).
Функциия принадлежности (membership function) – функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству.
Ц
Целенаправленность – наличие у системы цели (целей) и приоритет целей системы перед целями её элементов.
Э
Эксперимент – целенаправленное преобразование исследуемой системы (систем) для выявления ее (их) свойств.
Экспертные системы (Expert System) – это сложные программные комплексы, аккумулирующие знания специалистов в конкретных предметных областях и тиражирующие этот эмпирический опыт для консультаций менее квалифицированных пользователей..
Эксперты – это высококвалифицированные специалисты в данной предметной области, знания которых нужно передать экспертной системе.
Эмерджентность – появление у системы свойств, не присущих элементам системы; принципиальная несводимость свойства системы к сумме свойств составляющих её компонентов (неаддитивность).
Я
Ядро нечеткого множества – четкое подмножество универсального множества U, элементы которого имеют степени принадлежности равные единице: 